Periodische Vorgänge - Die allgemeine Sinusfunktion
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenDie allgemeine Form der Gleichung
Du kennst die normale Sinuskurve mit y = sin(x).
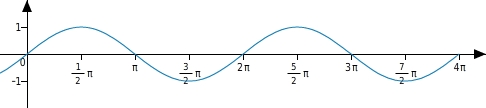 Durch die Verwendung von
Parameternkannst du die Gleichung verändern, um z.B. verschiedene periodische Vorgänge zu beschreiben oder zu modellieren.
Allgemein hat die Gleichung dann die Form:
y=a·sin(b(x+c))+d
Durch die Verwendung von
Parameternkannst du die Gleichung verändern, um z.B. verschiedene periodische Vorgänge zu beschreiben oder zu modellieren.
Allgemein hat die Gleichung dann die Form:
y=a·sin(b(x+c))+d
 Durch die Verwendung von
Parameternkannst du die Gleichung verändern, um z.B. verschiedene periodische Vorgänge zu beschreiben oder zu modellieren.
Allgemein hat die Gleichung dann die Form:
y=a·sin(b(x+c))+d
Durch die Verwendung von
Parameternkannst du die Gleichung verändern, um z.B. verschiedene periodische Vorgänge zu beschreiben oder zu modellieren.
Allgemein hat die Gleichung dann die Form:
y=a·sin(b(x+c))+d
y=3sin(-2(x-π))+1


Verschiebung entlang y-Achse
y=sin(x)+d
Der
Parameterd bewirkt eine
Verschiebungentlang der y-Achse.
Dadurch ändert sich der
Wertebereichund die Existenz und Lage von
Nullstellen.
Die
Periodeändert sich aber nicht.
 Der Parameter d hat folgende Wirkung auf die Sinuskurve:
Der Parameter d hat folgende Wirkung auf die Sinuskurve:


 Der Parameter d hat folgende Wirkung auf die Sinuskurve:
Der Parameter d hat folgende Wirkung auf die Sinuskurve:


Die Amplitude: Streckung oder Stauchung der Sinuskurve in y-Richtung
Der
Parametera wird im Allgemeinen Streckfaktor genannt.
Bei periodischen Funktionen mit nach oben und unten beschränktem Wertebereich wird der Betrag von a auch Amplitude genannt.
Durch den Parameter a wird der
Wertebereichverändert.
Die Lage der
Nullstellenändert sich aber nicht.
y=asin(x)
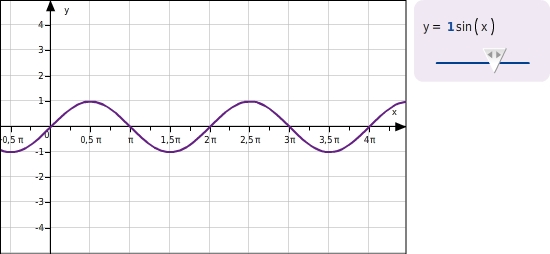 Der Parameter a hat folgende Wirkung auf die Sinuskurve:
Der Parameter a hat folgende Wirkung auf die Sinuskurve:

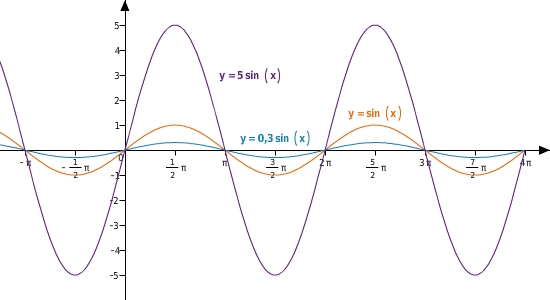
 Der Parameter a hat folgende Wirkung auf die Sinuskurve:
Der Parameter a hat folgende Wirkung auf die Sinuskurve:


Die Phase: Verschiebung der Sinuskurve in x-Richtung
Der
Parameterc wird auch Phase genannt.
Durch diesen Parameter ändert sich die Lage der
Nullstellenund der
Extremstellen.
Der
Wertebereichändert sich aber nicht.
y=sin(x+c)
 Der Parameter c hat folgende Wirkung auf die Sinuskurve:
Der Parameter c hat folgende Wirkung auf die Sinuskurve:
 Aufgrund der
Periode
2 πkann die
Phasenverschiebungnur bis
2 πan der Lage der
Hoch-bzw.
Tiefpunkteabgelesen werden.
Aufgrund der
Periode
2 πkann die
Phasenverschiebungnur bis
2 πan der Lage der
Hoch-bzw.
Tiefpunkteabgelesen werden.
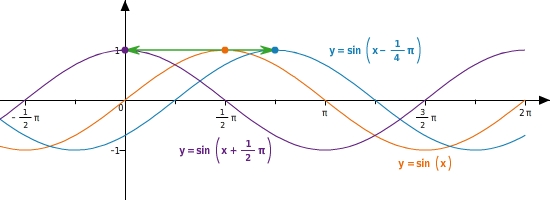
 Der Parameter c hat folgende Wirkung auf die Sinuskurve:
Der Parameter c hat folgende Wirkung auf die Sinuskurve:
 Aufgrund der
Periode
2 πkann die
Phasenverschiebungnur bis
2 πan der Lage der
Hoch-bzw.
Tiefpunkteabgelesen werden.
Aufgrund der
Periode
2 πkann die
Phasenverschiebungnur bis
2 πan der Lage der
Hoch-bzw.
Tiefpunkteabgelesen werden.

Die Periode: Streckung oder Stauchung der Sinuskurve in x-Richtung
y=sin(bx)
Der
Parameterb bewirkt eine Streckung oder Stauchung entlang der x-Achse.
Durch den Parameter b wird die
Periodeund damit die Lage der
Nullstellenverändert.
Der
Wertebereichändert sich aber nicht.
 Der Parameter b hat folgende Wirkung auf die Sinuskurve:
Der Parameter b hat folgende Wirkung auf die Sinuskurve:
 Die neue Periode T ergibt sich aus der Periode der Sinuskurve und dem Parameter b:
T=2π|b|
Die neue Periode T ergibt sich aus der Periode der Sinuskurve und dem Parameter b:
T=2π|b|

 Der Parameter b hat folgende Wirkung auf die Sinuskurve:
Der Parameter b hat folgende Wirkung auf die Sinuskurve:
 Die neue Periode T ergibt sich aus der Periode der Sinuskurve und dem Parameter b:
T=2π|b|
Die neue Periode T ergibt sich aus der Periode der Sinuskurve und dem Parameter b:
T=2π|b|

Kombination verschiedener Parameter
Verschiebung und Streckung lassen sich auch kombinieren.
Probiere es aus.



