+49 30 300 2440 00
 – Mo bis Fr von 8:30 - 17 Uhr

Mittelwert, Median, Modus

Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahren
Hier erfährst du, was die Lageparameter Modus, Median und Mittelwert bedeuten, wie du sie bestimmst und welche Eigenschaften sie haben.

Modus

Der Modus (auch Modalwert genannt) einer Datenreihe ist das Merkmal bzw. der Wert mit der größten Häufigkeit.Es kann auch mehrere Modi geben, wenn zwei oder mehrere verschiedene Merkmale gleich oft am häufigsten vorkommen.
Merkmale wie zum Beispiel
/wp-content/uploads/media/kem_StochS_StochSBeSMMM_1.jpg
weisen keine „natürliche“ Ordnung auf.
Daten, die zu solchen Merkmalen gehören, fallen somit in Klassen (auch Kategorien genannt), die nicht sinnvoll sortiert werden können.
Anna und Jonas machen eine Umfrage zur Gewalt an ihrer Schule.
Sie befragen 85 Schüler der Schule nach der Gewaltart, die sie an ihrer Schule am häufigsten wahrnehmen.
/wp-content/uploads/media/kem_StochS_StochSBeSMMM_2.jpg
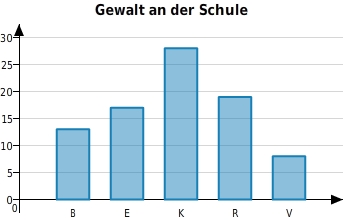
/wp-content/uploads/media/kem_StochS_StochSBeSMMM_3.jpg
Von Interesse ist hier der Modus der Datenreihe. Der Modus ist das Merkmal, das am häufigsten auftritt. In dem Säulendiagramm kannst du den Modus direkt ablesen. Zu ihm gehört die längste Säule./wp-content/uploads/media/kem_StochS_StochSBeSMMM_4.jpg Die Körperverletzung wurde am häufigsten (28-mal) genannt.

Median

Der Median (auch Zentralwert genannt) ist der Wert in der Mitte einer der Größe nach geordneten Datenreihe . Das heißt, mindestens 50 % der Daten sind kleiner als der Median oder gleich dem Median und mindestens 50 % der Daten sind größer als der Median oder gleich dem Median.
Der Median ist unempfindlich gegenüber Extremwerten.
Der Median wird verwendet für Daten, die in eine „natürliche“ Reihenfolge gebracht und mit Zahlenwerten versehen werden können.
Beispiele:
/wp-content/uploads/media/kem_StochS_StochSBeSMMM_5.jpg
Bei einer ungeraden Anzahl an Datenwerten ist der Median der Wert in der Mitte.
Bei einer geraden Anzahl an Datenwerten entspricht der Median dem Durchschnitt der beiden mittleren Werte.
Der Median ist die Mitte, bzw. der Zentralwert des Datensatzes.
Der Median wird genutzt, um einen einzelnen Wert der Datenreihe qualitativ einzuordnen.
Sophie möchte wissen, ob sie vergleichsweise viel oder weniger viel für die Mathematikarbeit gelernt hat.
Sie fragt ihre Klassenkameraden, wie viele Stunden sie jeweils gelernt haben.
/wp-content/uploads/media/kem_StochS_StochSBeSMMM_6.jpg
Um den Median zu bestimmen, sortierst du die Werte der Größe nach.
/wp-content/uploads/media/kem_StochS_StochSBeSMMM_7.jpg
Da hier eine ungerade Anzahl an Daten vorliegt, kannst du den Median direkt ablesen. Es ist der Wert in der Mitte (6).
Sophie hat mit 7 Stunden also eher viel für die Mathematikarbeit gelernt.
Paul Ulrich möchte wissen, ob seine Familie vergleichsweise viele oder wenige Kinder hat.
Er zählt, wie viele Kinder die Familien in seiner Nachbarschaft haben.
/wp-content/uploads/media/kem_StochS_StochSBeSMMM_8.jpg
Um den Median zu bestimmen, sortierst du die Werte der Größe nach.
/wp-content/uploads/media/kem_StochS_StochSBeSMMM_9.jpg
Da hier eine gerade Anzahl an Daten vorliegt, kannst du den Median nicht direkt ablesen. Du berechnest den Durchschnitt der beiden Werte in der Mitte:
  1 + 2 2 = 3 2 = 1.5
Pauls Familie hat mit zwei Kindern also vergleichsweise viele Kinder.

Mittelwert

Der Mittelwert eignet sich für quantitative Daten wie z.B. Körpergröße, Einkommen, Preise. Der Mittelwert ist empfindlich gegenüber Extremwerten.
Ausreißer innerhalb einer Datenreihe, "ziehen" den Mittelwert nach oben oder unten.
Den Mittelwert (auch arithmetisches Mittel genannt) berechnest du, indem du alle Beobachtungswerte x 1 , x 2 , ..., x n addierst und die Summe durch die Anzahl n der Beobachtungen dividierst:
  x _ = x 1 + x 2 + ... + x n n
Amelie macht in den Schulferien fünf Tage Urlaub bei ihrer Freundin.
Sie notiert sich jeden Tag, wie viel Taschengeld sie ausgegeben hat.
/wp-content/uploads/media/kem_StochS_StochSBeSMMM_10.jpg
Um die durchschnittlichen Ausgaben von Amelie zu bestimmen, berechnest du den Mittelwert:
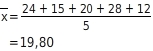/wp-content/uploads/media/kem_StochS_StochSBeSMMM_11.jpg
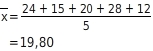Amelie hat also durchschnittlich 19.80 € am Tag ausgegeben.

Modus, Median und Mittelwert im Vergleich

Modus, Median und Mittelwert haben unterschiedliche Eigenschaften und eignen sich daher nicht für jede Art von Daten.
Ein neues Geschäft verkauft bedruckte T-Shirts in unterschiedlichen Farben.
Blaue T-Shirts wurden am häufigsten verkauft.
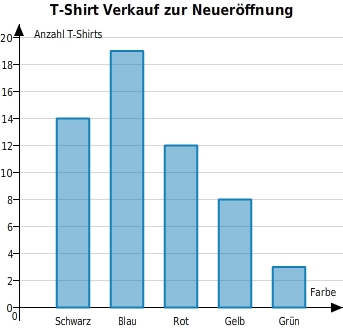
/wp-content/uploads/media/kem_StochS_StochSBeSMMM_12.jpg
Die Farbe Blau ist der Modus.
Einen Mittelwert oder den Median kannst du nicht bestimmen, denn die Daten (Merkmal: Farbe) lassen sich nicht in eine natürliche Reihenfolge bringen und als Zahlen angeben.
Lara hat im letzten Halbjahr ihre Englischzensuren notiert: 1, 2, 1, 3, 4, 2, 2, 3, 5.
Schreibt sie in der nächsten Englischarbeit eine 3, dann ist das für Lara eine eher schlechte Leistung.
Allerdings würde eine 3 ihre Note auf dem Zeugnis nicht beeinflussen.
Für die qualitative Einordnung der Note 3 in die Datenreihe, wählst du den Median als Lageparameter in der geordneten Datenreihe:
1, 1, 2, 2, 2, 3, 3, 4, 5 Median = 2
Die Zensur auf dem Zeugnis wird jedoch meist mit Hilfe des Mittelwertes ermittelt.
  1 + 1 + 2 + 2 + 2 + 3 + 3 + 4 + 5 9 ≈ 2.6
Lara bekäme also momentan eine 3 auf dem Zeugnis. Eine 3 in der nächsten Klassenarbeit würde daran nichts ändern, denn der Mittelwert wäre ebenfalls 2.6 .
Hätte sie statt der letzten 5 auch eine 3 bekommen, dann würde eine weitere 3 die Zeugnisnote gefährden, denn
  1 + 1 + 2 + 2 + 2 + 3 + 3 + 3 + 4 9 ≈ 2.3
Am Median hat sich nichts geändert. Lara bekäme also gerade so eine 2, aber die zusätzliche 3 würde sich negativ auswirken, denn der Mittelwert wäre 2.6 .
Sophie möchte wissen, ob sie vergleichsweise viel oder weniger viel für die Mathematikarbeit gelernt hat.
Sie fragt ihre Klassenkameraden, wie viele Stunden sie jeweils gelernt haben.
/wp-content/uploads/media/kem_StochS_StochSBeSMMM_13.jpg
Obwohl Sophie zu denen gehört, die eher viel gelernt haben, liegt sie mit ihrer Stundenzahl unter dem Durchschnitt.
Der Median ist 6 und Sophies Stundenzahl liegt über dem Median. Sie gehört also zu denen, die eher viel gelernt haben. Trotzdem liegt sie mit ihrer Stundenzahl unter dem Durchschnitt (ca. 7.3 Stunden).
Aber da Tom extrem viel gelernt hat, muss sein Wert als Ausreißer betrachtet werden, der den Durchschnitt stark beeinflusst und nach oben zieht. Ohne den Wert von Tom läge der Durchschnitt bei 5 Stunden ( 35 : 6 ≈ 5.8 ) und Sophie hätte überdurchschnittlich viel gelernt.