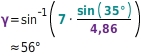Lösungsstrategien für Sinus- und Kosinussatz
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, unter welchen Voraussetzungen für die Berechnungen in Dreiecken die Anwendung des Sinussatzes oder die des Kosinussatzes die bessere Strategie ist.
Den richtigen Satz benutzen
Kennst du mindestens drei Größen (Seitenlängen und/oder Winkel) in einem beliebigen Dreieck, dann kannst du mindestens eineweitere Größe berechnen, indem du den oder den anwendest. Dabei kannst du mehrere Fälle unterscheiden: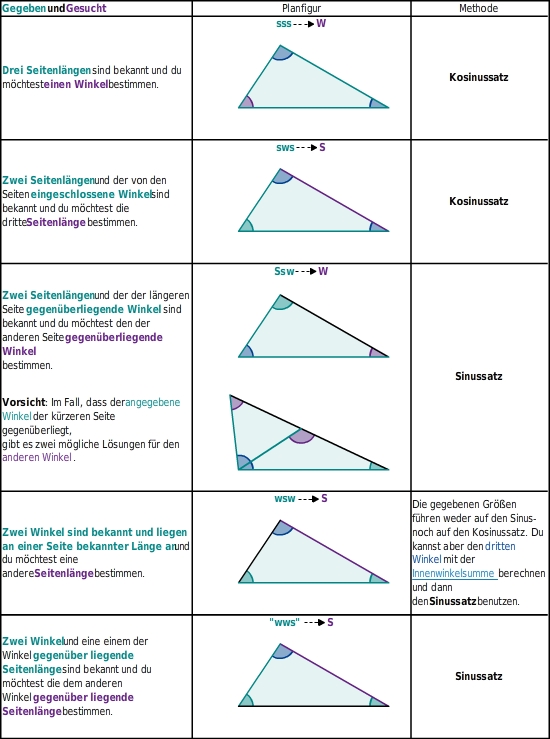 
Alle Größen im Dreieck berechnen
Möchtest du alle unbekannten Größen eines Dreiecks aus drei gegebenen Größen berechnen, gehst du strategisch vor.
Gegeben ist ein Dreieck mit zwei Seiten und dem eingeschlossenen Winkel. 
1. Entscheide, welcher der Fälle sss, sws, SsW oder wsw für die gegeben Größen vorliegt. sws 2. Wähle danach die dazu passende Strategie (Sinussatz oder Kosinussatz). Kosinussatz 3. Berechne damit eine vierte Größe. 
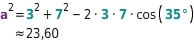Also: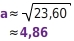 
4. Berechne alle weiteren Größen mit dem Sinussatz oder aus der . mit dem Sinussatz: 
Mit der Taste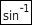 
deines Taschenrechners kannst du berechnen. 
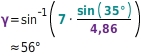mit der Innenwinkelsumme: 
1. Entscheide, welcher der Fälle sss, sws, SsW oder wsw für die gegeben Größen vorliegt. deines Taschenrechners kannst du berechnen. 
