Körperberechnung
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahren- Volumen eines Quaders berechnen
- Volumen eines Würfels berechnen
- Oberflächeninhalt eines Quaders berechnen
- Volumen eines Prismas berechnen
- Volumen eines Kegels berechnen
- Oberfläche eines Kegels berechnen
- Volumen eines Zylinders berechnen
- Oberfläche eines Zylinders berechnen
- Volumen einer Pyramide berechnen
- Oberfläche einer Pyramide berechnen
Volumen eines Quaders berechnen
Das
V eines
mit den Kantenlängen a, b und c berechnest du, indem du diese miteinander multiplizierst:


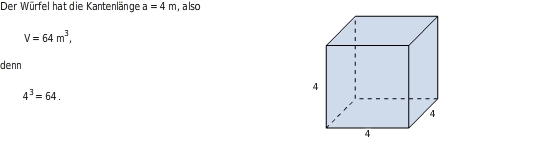
Volumen eines Würfels berechnen
Der
ist ein besonderer
.
Bei ihm sind alle zwölf Kanten gleich lang.
Für die Breite a, die Tiefe b und die Höhe c gilt
.
Für das Volumen gilt dann
.
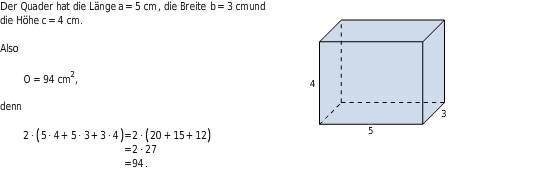
Oberflächeninhalt eines Quaders berechnen


Volumen eines Prismas berechnen
kurz:
Je nach Grundfläche des Prismas ergeben sich dann speziellere Formeln.
Prisma mit Dreieck ABC als Grundfläche (
,
) und einer Höhe h von






Mit der Formel zur Berechnung des Volumens kannst du auch die anderen Größen eines Prismas berechnen.
Du stellst die Formel mit Hilfe von äquivalenzumformungen nach der gesuchten Größe um:
 und
und
Volumen eines Kegels berechnen
kurz:
Die Grundfläche des Kegels ist ein
mit dem
r, daher ergibt sich die spezielle Formel
Kegel mit einer Höhe
von
und einem Radius
der Grundfläche von




Mit der Formel zur Berechnung des Volumens kannst du auch die anderen Größen eines Kegels berechnen.Du stellst die Formel mit Hilfe von äquivalenzumformungen nach der gesuchten Größe um:
 und
und
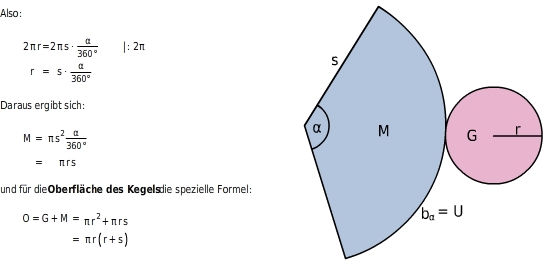
Oberfläche eines Kegels berechnen
kurz:
Die Oberfläche eines Kegels besteht aus der Grundfläche G und der Mantelfläche M.Die Grundfläche ist ein Kreis:
Der Mantel ist ein
mit der Bogenlänge
(
des Kreises) und dem Radius
(Mantellinie des Kegels):

Kegel mit einer Mantellinie s von
und einem Radius r von




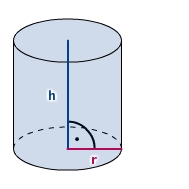
Volumen eines Zylinders berechnen
kurz:
Die Grundfläche des Zylinders ist ein Kreis mit
r, daher ergibt sich die spezielle Formel
.
Zylinder mit einer Höhe h von
und einem Radius r von



Mit der Formel zur Berechnung des Volumens kannst du auch die anderen Größen eines Zylinders berechnen.
Du stellst die Formel mit Hilfe von äquivalenzumformungen nach der gesuchten Größe um:
 und
und
Oberfläche eines Zylinders berechnen
kurz:
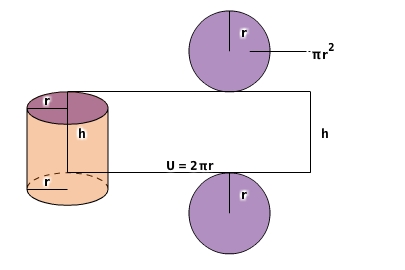
Die Oberfläche eines Zylinders setzt sich zusammen aus Grundfläche G, Deckfläche D und Mantelfläche M.
Grund- und Deckfläche sind gleich groß, also gilt:
Die Grundfläche ist ein
:
Der Mantel eines geraden Zylinders ist ein
mit der Seitenlänge U (Umfang des Kreises) und h (Höhe des Zylinders):
Für den Oberflächeninhalt des Zylinders gilt damit die spezifische Formel:

Zylinder mit einer Höhe h von
und einem Radius r von




Volumen einer Pyramide berechnen
Für das Volumen einer Pyramide gilt die Formel
Für die Berechnung der Grundfläche verwendest du dann die passende Flächeninhaltsformel.



Mit der Formel zur Berechnung des Volumens kannst du auch die anderen Größen einer Pyramide berechnen. Du stellst die Formel mit Hilfe von äquivalenzumformungen nach der gesuchten Größe um.
Nach
:
 oder nach
:
oder nach
:

Von einer Pyramide mit einem Volumen
von
und einer Grundfläche
von
wird die Höhe
(in cm) gesucht.
Du setzt die Werte für
und
in die Gleichung für
ein und berechnest
(in cm):


Oberfläche einer Pyramide berechnen
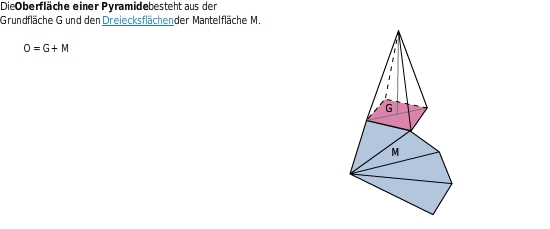
Pyramide mit quadratischer Grundfläche (a =
) und einer Seitenhöhe
von
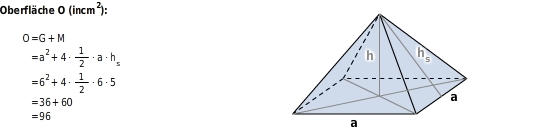
Mit der Formel zur Berechnung der Oberfläche kannst du auch Grundfläche und Mantelfläche berechnen. Dazu stellst du die Formel mit Hilfe von äquivalenzumformungen nach der gesuchten Größe um:
Nach
:
 oder nach
:
oder nach
:


