Euler, Leonhard
Name: Leonhard Euler
Geboren: 1707 in Basel
Gestorben: 1783 in Sankt Petersburg
Lehr-/Forschungsgebiete: Analysis, Algebra, Arithmetik, Infinitesimalrechnung, Graphentheorie, Variationsrechnung, Trigonometrie, Geometrie, Physik, Astronomie
Leonhard Euler war ein herausragender Mathematiker und Naturwissenschaftler, der im 18. Jahrhundert gelebt hat. Schweizerischen Ursprungs führte ihn seine wissenschaftliche Karriere nach Sankt Petersburg und Berlin. Für die Entwicklung der Mathematik hat Euler zahlreiche wichtige substantielle Entdeckungen und symbolische Beiträge geliefert. Unter anderem begründete er ein neues Teilgebiet der Mathematik, die Graphentheorie, und formulierte das Schlüsseltheorem der Variationsrechnung. Zu den nach ihm benannten Entdeckungen zählen die eulersche Zahlen, der Satz von Euler in der Zahlentheorie, der Satz von Euler in der Geometrie, die Eulergerade, die Euler-Formel, die Euler-Identität, die eulersche Funktion, die Euler-Mascheroni-Konstante, die Euler-Lagrange-Gleichung, die eulersche Polyederformel und einige weitere.
Leben
Leonhard Euler wurde 1707 in Basel als erster Sohn einer Pfarrersfamilie geboren. Ab 1720 studierte er an der Universität Basel und hörte hier Vorlesungen von Johann Bernoulli. Im Alter von 20 Jahren wurde er an die Universität Sankt Petersburg berufen, um dort die Professur des verstorbenen Nikolaus II. Bernoulli zu übernehmen. Später erhielt er auch eine Professur für Physik. Ab 1740 war er auf dem rechten Auge blind. 1741 ging er auf Einladung Friedrichs II. an die Königlich-Preußische Akademie der Wissenschaften in Berlin. 25 Jahre später kehrte er mit seiner Frau und seinen 13 Kindern nach Sankt Petersburg zurück. Obwohl er 1771 vollständig erblindete veröffentlichte er bis zu seinem Tod 1783 in Petersburg noch zahlreiche wissenschaftliche Beiträge. Sein Lebenswerk umfasst über 800 Publikationen.
Beiträge zur Mathematik
Eulers Beiträge zur Wissenschaft sind so zahlreich, dass hier nur eine Auswahl auf dem Gebiet der Mathematik erwähnt werden kann. Schon sein Einfluss auf die mathematische Notation macht seine Bedeutung ersichtlich: die mathematischen Symbole für die Basis des natürlichen Logarithmus (e), die Kreiszahl Pi (π), die imaginäre Einheit (i), das Summenzeichen (∑) und f(x) als Darstellung für eine Funktion gehen auf ihn zurück. Mit der Publikation einer Lösung für das so genannte Königsberger Brückenproblem begründete Euler ein neues Teilgebiet der Mathematik, die Graphentheorie. Zwischen anderen mathematischen Teilgebieten fand er neue Verbindungen, wie zum Beispiel die Eulersche Identität, die die trigonometrischen Funktionen mit den komplexen Zahlen verbindet.
Euler erweiterte den Gebrauch von Logarithmen und führte die Gammafunktion ein. In der Zahlentheorie definierte er die eulersche -Funktion und wendete sie im Satz von Euler an, der eine Verallgemeinerung des kleinen Fermatschen Satzes darstellt. Euler bewies die Fermatsche Vermutung fu?r den Fall n = 3 und stellte eine Verallgemeinerung der Fermatschen Vermutung auf, die sich jedoch 1966 als falsch herausstellte.
Darüber hinaus verbindet sich Eulers Name mit der Euler-Mascheroni-Konstante und der Euler-Lagrange-Gleichung. Von der Euler-Mascheroni-Konstante weiß man bis heute nicht, ob es sich um eine rationale oder irrationale Zahl handelt. Die Euler-Lagrange-Gleichung ist das Schlüsseltheorem der Variationsrechnung.
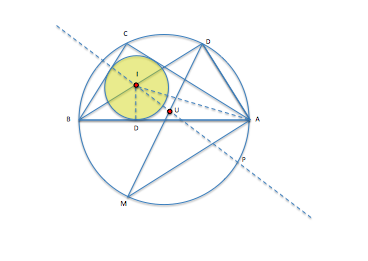
In der Geometrie bewies Euler unter anderem die Eulersche Polyederformel und den Satz von Euler. Letzter macht eine Aussage über die Entfernung d der Mittelpunkte von Umkreis und Inkreis eines Dreiecks. Als Eulersche Gerade bezeichnet man die Gerade, die durch den Schwerpunkt, den Umkreismittelpunkt und den Höhenschnittpunkt eines Dreiecks geht.
Bildquelle: Wikipedia

