+49 30 300 2440 00 – Mo bis Fr von 8:30 - 17 Uhr

Zur bettermarks Startseite
Auswahl
Schließen
RegistrierenEinloggen

Elementare Beziehungen zwischen Sinus, Kosinus und Tangens und besondere Winkel

Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahren
Hier erfährst du, welche Zusammenhänge zwischen den Winkeln in einem rechtwinkligen Dreieck bestehen und wie du diese ausnutzen kannst um andere Größen des Dreiecks zu berechnen.

Elementare Beziehungen zwischen Sinus und Kosinus

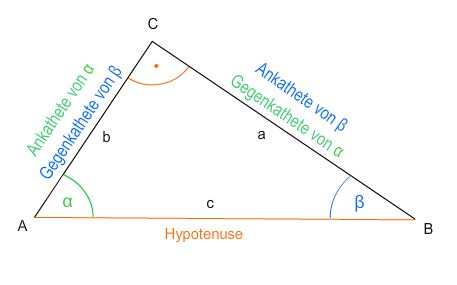
In einem rechtwinkligen Dreieck ABC mit dem rechten Winkel im Punkt C gilt:
Merksatz 1:
/wp-content/uploads/media/kem_Tri_TriBaDBez_1.jpg
Merksatz 2:
/wp-content/uploads/media/kem_Tri_TriBaDBez_2.jpg
Die Gegenkathete des Winkels α ist die Ankathete des Winkels β.
Aus der Innenwinkelsumme im Dreieck ( α + β + γ = 180 °) folgt für ein rechtwinkliges Dreieck mit γ = 90 °:
α + β = 90 °
Also:
β = 90 ° - α
und damit:
sin 90 ° - α = cos α
und
cos 90 ° - α = sin α
/wp-content/uploads/media/kem_Tri_TriBaDBez_4.jpg
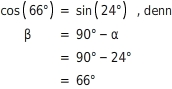
/wp-content/uploads/media/kem_Tri_TriBaDBez_5.jpg
Das gilt auch, wenn du α und β vertauschst.Natürlich kannst du auch den Taschenrechner verwenden.Du berechnest den Sinus von 24 ° und verwendest dann die Taste cos -1 : β = cos -1 sin 24 °

sin²(α) + cos²(α) = 1

Es gibt einen weiteren wichtigen Zusammenhang zwischen Sinus und Kosinus eines Winkels:
Merksatz 3:
Für jeden spitzen Winkel α gilt:
sin 2 α + cos 2 α = 1
(dabei ist sin 2 α = sin α 2 und cos 2 α = cos α 2 )
Das lässt sich an einem rechtwinkligen Dreieck schnell herleiten:
/wp-content/uploads/media/kem_Tri_TriBaDBez_6.jpg
Satz des Pythagoras: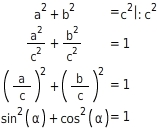
/wp-content/uploads/media/kem_Tri_TriBaDBez_7.jpg
Wähle einen beliebigen Winkel α und überprüfe die Gleichheit mit deinem Taschenrechner.
Mit Hilfe dieser Beziehung kannst du ohne Taschenrechner zu jedem Winkel den Sinus aus dem Kosinus oder den Kosinus aus dem Sinus bestimmen.
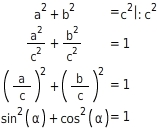
Wenn sin α = 0.6 , dann cos α = 0.8 .
Du stellst
sin 2 α + cos 2 α = 1
nach cos α um:
cos 2 α = 1 - sin 2 α
Also:
/wp-content/uploads/media/kem_Tri_TriBaDBez_8.jpg

Der Tangens als Quotient aus Sinus und Kosinus

/wp-content/uploads/media/kem_Tri_TriBaDBez_9.jpg
Merksatz 4:
In einem rechtwinkligen Dreieck ABC mit γ = 90 " gilt:
tan α = sin α cos α
Wenn sin α = 0.6 , dann tan α = 0.75 .
Du ersetzt in
tan α = sin α cos α
cos α durch 1 - sin 2 α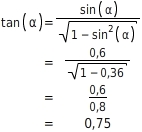
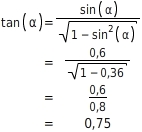
/wp-content/uploads/media/kem_Tri_TriBaDBez_11.jpg

Der Tangens, Sinus und Kosinus von 45°, 30° und 60°

/wp-content/uploads/media/kem_Tri_TriBaDBez_12.jpg
Zu einigen Winkeln ergeben sich Werte für Sinus, Kosinus und Tangens, die du dir leicht merken kannst.
/wp-content/uploads/media/kem_Tri_TriBaDBez_13.jpg

Erfolgreich Mathe lernen mit bettermarks

Die adaptiven Übungen von bettermarks können Schülerinnen und Schüler auf dem Tablet, dem Computer und dem Smartphone rechnen und bekommen personalisierte Rückmeldungen.

Wirkung wissenschaftlich bewiesen

Die Regierung von Uruguay hat eine dreijährige Studie auf Basis von UNESCO-Daten zur Nutzung von bettermarks durchgeführt. Das Ergebnis: Bis zu 30% Lernzuwachs.

Über 130 Millionen gerechnete Aufgaben pro Jahr

In Deutschland rechneten im Schuljahr 20/21 über 400.000 Schülerinnen und Schüler mit bettermarks. Dabei wurden mehr als 144 Millionen Aufgaben gelöst.

In Schulen in über zehn Ländern weltweit im Einsatz

bettermarks ist in vier Sprachen verfügbar und wird unter anderem in Deutschland, den Niederlanden, Uruguay und Südafrika täglich im Unterricht eingesetzt.

smartphonemenu-circle