Einfache Trigonometrie

Da rechtwinklige Dreiecke mit gleich großen Winkeln ähnlich zueinander sind, sind die Seitenverhältnisse eindeutig durch einen der beiden spitzen Winkel festgelegt.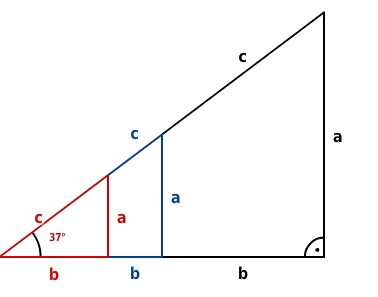

Je nach Wahl des Winkels bekommen die Seiten im rechtwinkligen Dreieck „neue Namen“.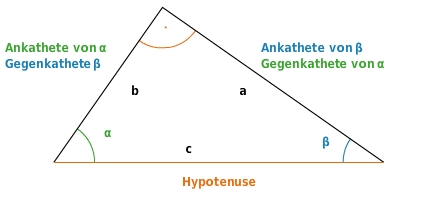Die Zuordnungen „Winkel“ -> „Seitenverhältnis“ sind eindeutig und definieren die Winkelfunktionen Sinus, Kosinus und Tangens für jeden der beiden spitzen Winkel $\alpha$ und ß. Der Sinus eines Winkels ist das Längenverhältnis von Gegenkathete zu Hypotenuse: $\text{Sinus}=\frac{\text{Gegenkathete}}{\text{Hypotenuse}}$ Der Kosinus eines Winkels ist das Längenverhältnis von Ankathete zu Hypotenuse: $\text{Kosinus}=\frac{\text{Ankathete}}{\text{Hypotenuse}}$ Der Tangens eines Winkels ist das Längenverhältnis von Gegenkathete zu Ankathete: $\text{Tangens}=\frac{\text{Gegenkathete}}{\text{Ankathete}}$

Mit Hilfe der Winkelfunktionen kannst du Winkel und Seitenlängen im rechtwinkligen Dreieck berechnen.Aus der Angabe nur eines Winkels (nicht dem rechten) und einer Seitenlänge kannst du die beiden anderen Seitenlängen und den dritten Winkel (durch Ergänzen auf $90°$) berechnen.

Für die Winkelfunktionen gibt es auf den meisten Taschenrechnern entsprechende Tasten. Je nach Fabrikat wählst du erst die Funktion und dann das Argument (den Winkel) oder umgekehrt.

Hast du den Funktionswert (das Längenverhältnis) gegeben, dann verwendest du für die Berechnung des Arguments(des Winkels) die „Umkehrfunktion“. In den meisten Fällen steht die Umkehrfunktion über den Tasten der zugehörigen Funktion. Um diese Umkehrfunktionen anwählen zu können, benutzt du die Umschalt-Taste. Oft ist sie in einer anderen Farbe und beschriftet mit „Shift“ oder „INV“.

Ein Haus ist $8.5m$ breit und das Dach hat eine Neigung von $50°$. Wie hoch ist der Dachgiebel (in m)? 1. Lösungsplan 2. Gleichung aufstellenDie Höhe h teilt das gleichschenklige Giebeldreieck in zwei kongruente rechtwinklige Dreiecke, von denen ein Winkel ( $\alpha$) und die Länge der Ankathete $\frac{\text{b}}{2}$ bekannt sind. 3. Gleichung lösen