Der Sinussatz
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenHier erfährst du, wie du mit dem Sinussatz Seitenlängen und Winkel in beliebigen Dreiecken berechnen kannst.
Der Sinussatz
Das Verhältnis der Längen zweier Seiten ist gleich dem Verhältnis der
ihrer gegenüberliegenden Winkel.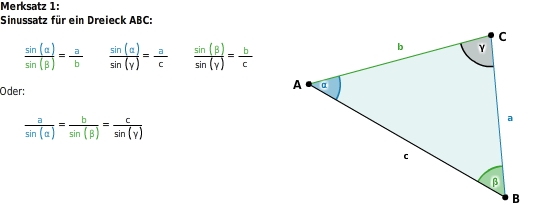

Seitenlängen berechnen
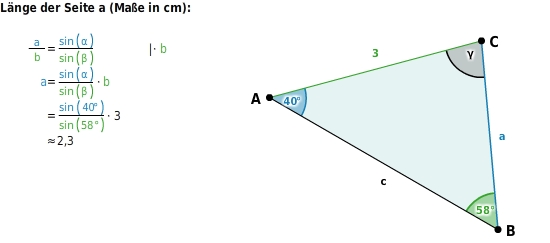
Mit dem Sinussatz kannst du aus zwei Winkeln und der Länge einer der beiden gegenüberliegenden Seiten (sww) die Länge der anderen gegenüberliegenden Seite berechnen.
Dreieck ABC mit der Länge der Seite
und den Winkeln
und

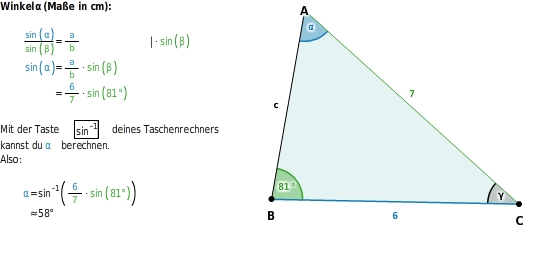
Winkel berechnen
Mit dem Sinussatz kannst du aus den Längen zweier Seiten und dem der längeren Seite gegenüberliegenden Winkel (Ssw) den anderen gegenüberliegenden Winkel berechnen.
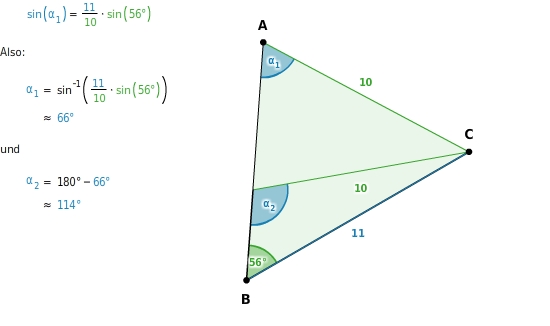
Vorsicht:
Hast du den der kürzeren Seite gegenüberliegenden Winkel gegeben, gibt es zwei mögliche Winkel (und Dreiecke), die du mit dem Sinussatz berechnen kannst.

Im Dreieck ABC liegt
der kürzeren Seite (10) gegenüber. Es gibt also zwei Dreiecke mit diesen Größen.