Anwendungen zu linearen Gleichungssystemen
Online Mathe üben mit bettermarks
- Über 2.000 Übungen mit über 100.000 Aufgaben
- Interaktive Eingaben, Lösungswege und Tipps
- Automatische Auswertungen und Korrektur
- Erkennung von Wissenslücken
Hier erfährst du, wie du Textaufgaben mit Hilfe von linearen Gleichungssystemen lösen kannst.
Lösen von Anwendungsaufgaben Schritt für Schritt
Bei Textaufgaben ist es hilfreich, Schritt für Schritt vorzugehen.
1. Variablen einführenDu überlegst, was mit Hilfe der Variablen beschrieben werden soll.
2. Gleichungen aufstellenDu überlegst, wie die Größen, für die du die Variablen gewählt hast, miteinander in Beziehung stehen und wie du diese Beziehungen durch Gleichungen formulieren kannst.
3. Gleichungssystem lösenDu löst das dabei entstehende lineare Gleichungssystem.
4.Ergebnis am Sachverhalt überprüfenDu überprüfst, ob die Lösung des Gleichungssystems auch eine Lösung für die konkrete Fragestellung ist.
Zahlenrätsel
Gesucht sind zwei positive ganze Zahlen.Die Summe aus dem Doppelten der einen Zahl und dem Vierfachen der anderen Zahl ist 50. Die Summe aus dem Vierfachen der einen Zahl und dem Doppelten der anderen Zahl ist 46.
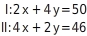
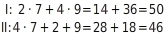
Variablen einführen
Du kannst auch andere Buchstaben als Variablen wählen.
Zahl 1:
Zahl 2:
Gleichungen aufstellen
bzw.
bedeutet, dass die jeweilige Variable mit 2 bzw. 4 multipliziert wird.Die Summe ist das Ergebnis der Addition.
Gleichungssystem lösen
Du stellst die Gleichung I nach
um:
Den Term auf der rechten Seite der Gleichung setzt du für
in die Gleichung II ein und berechnest
:
in II:
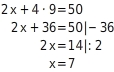
Diesen Wert setzt du für
in Gleichung I ein und berechnest
:
in I:
Diesen Wert setzt du für
in Gleichung I ein und berechnest
:
in I: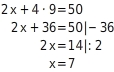
L = 7 ; 9
Ergebnis am Sachverhalt überprüfen
Beide Zahlen sind positiv, so wie es in der Aufgabenstellung gefragt war.Um festzustellen, ob die Ergebnisse auch richtig sind, setzt du die Werte für
und
in beide Gleichungen ein und überprüfst, ob wahre Aussagen entstehen.
Mischungsaufgabe
Ein Apotheker hat 36
igen und 21
igen Alkohol. Welche Mengen von beiden Lösungen muss er mischen, um 5 Liter 30
igen Alkohol zu erhalten?
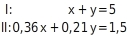
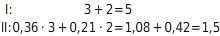
Variablen einführen
Du kannst auch andere Buchstaben als Variablen wählen.
Menge 36
iger Alkohol:
Menge 21
iger Alkohol:
Gleichungen aufstellen
Der Apotheker möchte 5 Liter Mischung herstellen. Die Summe der beiden Teilmengen muss 5 Liter ergeben.Die Mischung soll 30
Alkohol enthalten. In 5 Litern Mischung sind demnach 1,5 Liter Alkohol (
).36
von
und 21
von
müssen also 1,5 ergeben.
Gleichungssystem lösen
Du stellst die Gleichung I nach
um:
Den Term auf der rechten Seite der Gleichung setzt du für
in die Gleichung II ein und berechnest
:
in II:
Diesen Wert setzt du für
in Gleichung I ein und berechnest
:y in I:
Diesen Wert setzt du für
in Gleichung I ein und berechnest
:y in I:
L = 3 ; 2
Ergebnis am Sachverhalt überprüfen
Du setzt die Werte für
und
in beide Gleichungen ein und überprüfst, ob wahre Aussagen entstehen.