Addition und Subtraktion von rationalen Zahlen
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenIn diesen Erklärungen erfährst du, wie du rationale Zahlen addierst und subtrahierst.
Vorzeichen und Rechenzeichen
Eine rationale Zahl kann auch negativ sein. Um in Rechnungen Vor- und Rechenzeichen unterscheiden zu können, setzt man um die Zahl mit dem zugehörigen Vorzeichen eine Klammer: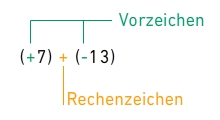
Um die Schreibweise zu vereinfachen, verwendet man die Klammern oft nur, wenn Rechenzeichen und Vorzeichen aufeinandertreffen.
Statt (+7) + (-13) wird also +7 + (-13) geschrieben.
Das Vorzeichen bei positiven Zahlen (+) wird ebenfalls häufig weggelassen, um die Schreibweise noch weiter zu vereinfachen.
Statt (+7) + (-13) wird also 7 + (-13)
Weitere Beispiele zur Vereinfachung der Schreibweise:
Statt (+9) - (+4) wird also 9 - 4 geschrieben.
Statt (+11) - (-8) wird also 11 - (-8) geschrieben.
Rationale Zahlen addieren
Wenn du zu einer rationalen Zahl eine positive Zahl addierst, gehst du auf der Zahlengeraden um den Betrag dieser Zahl nach rechts
Wenn du zu einer rationalen Zahl eine negative Zahl addierst, gehst du auf der Zahlengeraden um den Betrag dieser Zahl nach links.
Rationale Zahlen subtrahieren
Wenn du von einer rationalen Zahl eine positive Zahl subtrahierst, gehst du auf der Zahlengeraden nach links. Stellst du die Aufgabe vereinfacht dar, erkennst du, dass sie sich nicht von den dir bekannten Subtraktionsaufgaben unterscheidet.
Wenn du von einer rationalen Zahl eine negative Zahl subtrahierst, gehst du auf der Zahlengeraden nach rechts. Denn du subtrahierst eine negative Zahl, indem du ihre Gegenzahl addierst.
Rechenausdrücke mit rationalen Zahlen vereinfachen
Aus kompliziert scheinenden Rechnungen kannst du mit den folgenden Tipps übersichtliche Rechnungen machen, die du dann leichter lösen kannst.
Rationale Zahlen geschickt addieren
Um Additionsaufgaben mit mehreren rationalen Zahlen geschickt zu lösen, helfen dir oft die beiden folgenden Gesetze weiter: Das Kommutativgesetz (Vertauschungsgesetz) erlaubt dir, die Reihenfolge der Summanden zu vertauschen: Das Assoziativgesetz (Verbindungsgesetz) erlaubt dir, in einer Summe mit mehreren Summanden beliebig Klammern zu setzen oder zu entfernen, um bestimmte Teilaufgaben zuerst zu rechnen: Deshalb werden Rechenausdrücke, in denen nur das Pluszeichen vorkommt, oft ganz ohne Klammern geschrieben.
Wenn du diese Gesetze geschickt anwendest, kann dir das die Lösung einer Aufgabe erleichtern.
