Relative Häufigkeiten und Wahrscheinlichkeiten
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahrenErweiterung von Baumdiagrammen zu Wahrscheinlichkeitsbäumen
Baumdiagramme können durch eine kleine Erweiterung sehr geschickt zur Berechnung von Wahrscheinlichkeiten von Ereignissen mehrstufiger Zufallsexperimente benutzt werden.
Dazu trägst du an den Zweigen die jeweiligen Wahrscheinlichkeiten ein, mit denen das zum Zweig gehörige Ergebnis des Teilexperimentes eintritt. Diese Wahrscheinlichkeiten nennt man kurz Zweigwahrscheinlichkeiten.
Ein Baumdiagramm, das Zweigwahrscheinlichkeiten enthält, nennt man auch kurz Wahrscheinlichkeitsbaum. üblicherweise gibt man alle Zweigwahrscheinlichkeiten entweder komplett als Brüche oder Dezimalzahlen an.
Zweimaliges Ziehen aus einer Urne ohne Zurücklegen
Du kannst den Wahrscheinlichkeitsbaum zu folgendem Zufallsexperiment konstruieren:Aus der abgebildeten Urne werden nacheinander 2 Kugeln gezogen, ohne sie zurückzulegen.Ein passendes Baumdiagramm ist zum Beispiel:
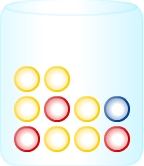


Beachte hierbei, dass die Farbe Blau nur einmal vorkommt und die gezogenen Kugeln nicht zurückgelegt werden. Daher gibt es keinen Zweig zu Blau, nachdem Blau gezogen wurde.
Jeder Zweig im Baumdiagramm entspricht einem Ergebnis eines der beiden Teilexperimente „Ziehen der ersten Kugel aus der Urne“ bzw. „Ziehen der zweiten Kugel aus der Urne „.
Eine Zweigwahrscheinlichkeit ist die Wahrscheinlichkeit dafür, dass das zum jeweiligen Zweig gehörige Ergebnis eintritt.
Beim Ziehen der ersten Kugel sind die möglichen Ergebnisse
 ,
,  und
und  .
Beim ersten Ziehen kann jede Kugel mit derselben Wahrscheinlichkeit (
110) gezogen werden.
Daher kannst du die Wahrscheinlichkeiten der Ergebnisse
.
Beim ersten Ziehen kann jede Kugel mit derselben Wahrscheinlichkeit (
110) gezogen werden.
Daher kannst du die Wahrscheinlichkeiten der Ergebnisse  ,
,  und
und  mit Hilfe der Formel für Laplace-Wahrscheinlichkeiten berechnen:
Erste Ziehung
Wahrscheinlichkeit von Teilergebnis
mit Hilfe der Formel für Laplace-Wahrscheinlichkeiten berechnen:
Erste Ziehung
Wahrscheinlichkeit von Teilergebnis  :
310Wahrscheinlichkeit von Teilergebnis
:
310Wahrscheinlichkeit von Teilergebnis  :
610=
35Wahrscheinlichkeit von Teilergebnis
:
610=
35Wahrscheinlichkeit von Teilergebnis  :
110
:
110
 Die Wahrscheinlichkeiten der Teilergebnisse
Die Wahrscheinlichkeiten der Teilergebnisse  ,
,  und
und  für die zweite Ziehung sind nun abhängig vom Ausgang der ersten Ziehung. Je nachdem fehlt nun eine der Kugeln der Farbe
für die zweite Ziehung sind nun abhängig vom Ausgang der ersten Ziehung. Je nachdem fehlt nun eine der Kugeln der Farbe  ,
,  bzw.
bzw.  .
Zweite Ziehung
Falls die erste Ziehung
.
Zweite Ziehung
Falls die erste Ziehung  lieferte:Wahrscheinlichkeit von Teilergebnis
lieferte:Wahrscheinlichkeit von Teilergebnis  :
29Wahrscheinlichkeit von Teilergebnis
:
29Wahrscheinlichkeit von Teilergebnis  :
69=
23Wahrscheinlichkeit von Teilergebnis
:
69=
23Wahrscheinlichkeit von Teilergebnis  :
19
Falls die erste Ziehung
:
19
Falls die erste Ziehung  lieferte:Wahrscheinlichkeit von Teilergebnis
lieferte:Wahrscheinlichkeit von Teilergebnis  :
39=
13Wahrscheinlichkeit von Teilergebnis
:
39=
13Wahrscheinlichkeit von Teilergebnis  :
59Wahrscheinlichkeit von Teilergebnis
:
59Wahrscheinlichkeit von Teilergebnis  :
19
Falls die erste Ziehung
:
19
Falls die erste Ziehung  lieferte:Wahrscheinlichkeit von Teilergebnis
lieferte:Wahrscheinlichkeit von Teilergebnis  :
39=
13Wahrscheinlichkeit von Teilergebnis
:
39=
13Wahrscheinlichkeit von Teilergebnis  :
69=
23
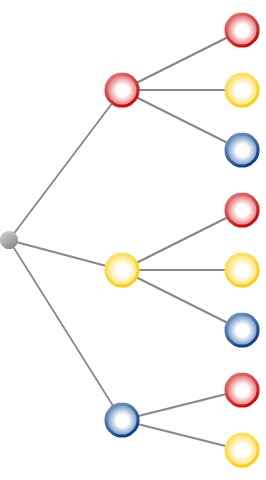
Nach dem Eintragen aller Zweigwahrscheinlichkeiten sieht der Wahrscheinlichkeitsbaum wie folgt aus:
:
69=
23
Nach dem Eintragen aller Zweigwahrscheinlichkeiten sieht der Wahrscheinlichkeitsbaum wie folgt aus:

 Die Wahrscheinlichkeiten der Teilergebnisse
Die Wahrscheinlichkeiten der Teilergebnisse 
Ereigniswahrscheinlichkeiten mit Wahrscheinlichkeitsbäumen berechnen
Wenn du ein Baumdiagramm zu einem Wahrscheinlichkeitsbaum erweitert hast, kannst du diesen Baum nutzen, um Wahrscheinlichkeiten von Ereignissen des zugehörigen Zufallsexperimentes zu berechnen.
Dazu markierst du alle Ergebnisse des mehrstufigen Zufallsexperimentes, die zu einem interessierenden Ereignis gehören und ermittelst für diese die zugehörigen Pfadwahrscheinlichkeiten.
Zum Schluss addierst du diese Pfadwahrscheinlichkeiten.
Aus der abgebildeten Urne werden nacheinander 2 Kugeln gezogen, ohne sie zurückzulegen. Ein zugehöriger Wahrscheinlichkeitsbaum ist angegeben:

 Du berechnest die Wahrscheinlichkeit des Ereignisses E „Genau eine Kugel hat die Farbe Gelb“, indem du zuerst die zum Ereignis E - „Genau eine Kugel hat die Farbe Gelb“ - gehörigen Ergebnisse den entsprechenden Endknoten im Baum zuordnest:
Du berechnest die Wahrscheinlichkeit des Ereignisses E „Genau eine Kugel hat die Farbe Gelb“, indem du zuerst die zum Ereignis E - „Genau eine Kugel hat die Farbe Gelb“ - gehörigen Ergebnisse den entsprechenden Endknoten im Baum zuordnest:
 ;
; 
 ;
; 
 ;
; 

 Dann berechnest du für jedes zu E gehörige Ergebnis die Pfadwahrscheinlichkeit.
Dabei wendest du die Produktregel für Pfadwahrscheinlichkeiten an:
P(
Dann berechnest du für jedes zu E gehörige Ergebnis die Pfadwahrscheinlichkeit.
Dabei wendest du die Produktregel für Pfadwahrscheinlichkeiten an:
P(
 ) =
310·23=15
P(
) =
310·23=15
P(
 ) =
35·13=15
P(
) =
35·13=15
P(
 ) =
35·19=115
P(
) =
35·19=115
P(
 ) =
110·23=115
Diese Pfadwahrscheinlichkeiten schreibst du neben die zugehörigen Ergebnisse.
) =
110·23=115
Diese Pfadwahrscheinlichkeiten schreibst du neben die zugehörigen Ergebnisse.
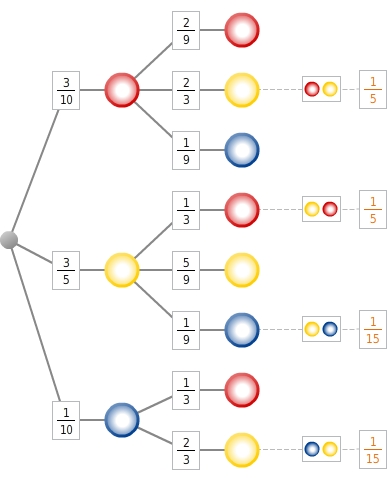 Du berechnest die Wahrscheinlichkeit des Ereignisses E ("Genau eine Kugel hat die Farbe Gelb"), indem du die Pfadwahrscheinlichkeiten der zu E gehörigen Ergebnisse addierst:
Du berechnest die Wahrscheinlichkeit des Ereignisses E ("Genau eine Kugel hat die Farbe Gelb"), indem du die Pfadwahrscheinlichkeiten der zu E gehörigen Ergebnisse addierst:


 Du berechnest die Wahrscheinlichkeit des Ereignisses E „Genau eine Kugel hat die Farbe Gelb“, indem du zuerst die zum Ereignis E - „Genau eine Kugel hat die Farbe Gelb“ - gehörigen Ergebnisse den entsprechenden Endknoten im Baum zuordnest:
Du berechnest die Wahrscheinlichkeit des Ereignisses E „Genau eine Kugel hat die Farbe Gelb“, indem du zuerst die zum Ereignis E - „Genau eine Kugel hat die Farbe Gelb“ - gehörigen Ergebnisse den entsprechenden Endknoten im Baum zuordnest: Dann berechnest du für jedes zu E gehörige Ergebnis die Pfadwahrscheinlichkeit.
Dabei wendest du die Produktregel für Pfadwahrscheinlichkeiten an:
P(
Dann berechnest du für jedes zu E gehörige Ergebnis die Pfadwahrscheinlichkeit.
Dabei wendest du die Produktregel für Pfadwahrscheinlichkeiten an:
P( Du berechnest die Wahrscheinlichkeit des Ereignisses E ("Genau eine Kugel hat die Farbe Gelb"), indem du die Pfadwahrscheinlichkeiten der zu E gehörigen Ergebnisse addierst:
Du berechnest die Wahrscheinlichkeit des Ereignisses E ("Genau eine Kugel hat die Farbe Gelb"), indem du die Pfadwahrscheinlichkeiten der zu E gehörigen Ergebnisse addierst:

Die beiden abgebildeten Glücksräder werden jeweils einmal gedreht. Zuerst wird das linke, dann das rechte Glücksrad gedreht.

 Berechne die Wahrscheinlichkeit für das Ereignis E „Die Räder bleiben auf derselben Farbe stehen“.Konstruiere dazu ein zum beschriebenen Zufallsexperiment gehöriges Baumdiagramm. Färbe dabei auch die Knoten entsprechend und gib an den Zweigen die zugehörigen Wahrscheinlichkeiten als Dezimalzahlen ein.
Berechne die Wahrscheinlichkeit für das Ereignis E „Die Räder bleiben auf derselben Farbe stehen“.Konstruiere dazu ein zum beschriebenen Zufallsexperiment gehöriges Baumdiagramm. Färbe dabei auch die Knoten entsprechend und gib an den Zweigen die zugehörigen Wahrscheinlichkeiten als Dezimalzahlen ein.

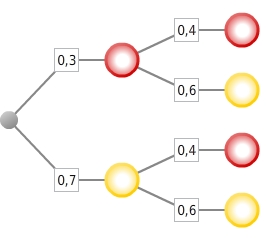



 Berechne die Wahrscheinlichkeit für das Ereignis E „Die Räder bleiben auf derselben Farbe stehen“.Konstruiere dazu ein zum beschriebenen Zufallsexperiment gehöriges Baumdiagramm. Färbe dabei auch die Knoten entsprechend und gib an den Zweigen die zugehörigen Wahrscheinlichkeiten als Dezimalzahlen ein.
Berechne die Wahrscheinlichkeit für das Ereignis E „Die Räder bleiben auf derselben Farbe stehen“.Konstruiere dazu ein zum beschriebenen Zufallsexperiment gehöriges Baumdiagramm. Färbe dabei auch die Knoten entsprechend und gib an den Zweigen die zugehörigen Wahrscheinlichkeiten als Dezimalzahlen ein.
Baumdiagramm konstruieren
Die vom Startknoten ausgehenden Zweige führen zu den Knoten, die den möglichen Ergebnissen des ersten Teilexperimentes „Drehen am linken Glücksrad“ entsprechen:
 und
und  .
Dabei spielt die Reihenfolge der Zweige bzw. Knoten keine Rolle.
In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Drehen am rechten Glücksrad“ führen:
.
Dabei spielt die Reihenfolge der Zweige bzw. Knoten keine Rolle.
In gleicher Weise gehen von den Knoten, die die Ergebnisse des ersten Teilexperimentes darstellen, diejenigen Zweige aus, die nun zu den möglichen Ergebnissen des zweiten Teilexperimentes „Drehen am rechten Glücksrad“ führen:
 und
und  .
Wiederum spielt dabei die Reihenfolge der Zweige bzw. Knoten keine Rolle.
.
Wiederum spielt dabei die Reihenfolge der Zweige bzw. Knoten keine Rolle.

Zweigwahrscheinlichkeiten ergänzen
Eine Zweigwahrscheinlichkeit ist die Wahrscheinlichkeit dafür, dass das zum jeweiligen Zweig gehörige Ergebnis eintritt.
Beim Drehen sowohl des linken Glücksrades als auch des rechten Glücksrades sind die möglichen Ergebnisse  und
und  .
Da für die beiden Glücksräder jeder Sektor mit gleicher Wahrscheinlichkeit (
110bzw.
15) gedreht werden kann, berechnest du die Wahrscheinlichkeiten der Teilergebnisse
.
Da für die beiden Glücksräder jeder Sektor mit gleicher Wahrscheinlichkeit (
110bzw.
15) gedreht werden kann, berechnest du die Wahrscheinlichkeiten der Teilergebnisse  und
und  für die beiden Glücksräder mit Hilfe der Formel für Laplace-Wahrscheinlichkeiten:
Drehen des linken Glücksrades:Wahrscheinlichkeit von Teilergebnis
für die beiden Glücksräder mit Hilfe der Formel für Laplace-Wahrscheinlichkeiten:
Drehen des linken Glücksrades:Wahrscheinlichkeit von Teilergebnis  :
310= 0,3Wahrscheinlichkeit von Teilergebnis
:
310= 0,3Wahrscheinlichkeit von Teilergebnis  :
710= 0,7
Drehen des rechten Glücksrades:Wahrscheinlichkeit von Teilergebnis
:
710= 0,7
Drehen des rechten Glücksrades:Wahrscheinlichkeit von Teilergebnis  :
25= 0,4Wahrscheinlichkeit von Teilergebnis
:
25= 0,4Wahrscheinlichkeit von Teilergebnis  :
35= 0,6
:
35= 0,6

Ergebnisse auswählen
Du ziehst alle diejenigen Ergebnisse an die entsprechenden Positionen im Baum, die zu dem Ereignis E „Die Räder bleiben auf derselben Farbe stehen“ gehören:

 und
und 
 .
.

Pfadwahrscheinlichkeiten ermitteln
Du berechnest die Pfadwahrscheinlichkeiten mit Hilfe der Produktregel. Du multiplizierst also die Zweigwahrscheinlichkeiten der Pfade, die zu den zum Ereignis E gehörenden Ergebnissen führen.
P(
 ) = 0,3
·0,4 = 0,12P(
) = 0,3
·0,4 = 0,12P(
 ) = 0,7
·0,6 = 0,42
) = 0,7
·0,6 = 0,42

Wahrscheinlichkeit berechnen
Du ermittelst die Wahrscheinlichkeit eines Ereignisses mit Hilfe eines Wahrscheinlichkeitsbaumes, indem du die Pfadwahrscheinlichkeiten der zum Ereignis gehörigen Ergebnisse addierst.
P(E) = P(
 ) + P(
) + P(
 ) = 0,12 + 0,42 = 0,54
) = 0,12 + 0,42 = 0,54
P(E) = 0,54
Laplace-Wahrscheinlichkeiten und daraus resultierende Regeln
Ein Zufallsexperiment eines Wahrscheinlichkeitsraumes mit Ergebnismenge Ω wird als Laplace-Experiment bezeichnet, falls jedes Ergebnis a ∈ Ω gleich wahrscheinlich ist.
Erkennen kannst du Laplace-Experimente meistens an vorliegenden Symmetrien, zum Beispiel der Form eines geworfenen Gegenstandes (Würfel, Münze) oder der Anordnung von Gewinnfeldern wie auf einem Roulette-Rad.
In einem Laplace-Experiment gilt für die Wahrscheinlichkeit P eines Ereignisses:
P =
Anzahl der für das Ereignis günstigen ErgebnisseAnzahl der möglichen Ergebnisse
Würfeln mit Ergebnismenge Ω = {1; 2; 3; 4; 5; 6} ist ein Laplace-Experiment, weil beim Würfeln mit einem „fairen“ Würfel aufgrund der symmetrischen Form und der gleichmäßig verteilten Masse des Würfels jede der sechs Seiten mit gleicher Wahrscheinlichkeit oben liegen bleibt.Jede Zahl wird also mit Wahrscheinlichkeit
16gewürfelt.
Würfeln mit Ergebnismenge Ω = {keine 6; 6} ist kein Laplace-Experiment, weil mit geringerer Wahrscheinlichkeit eine „6“ als „keine 6“, also eines der fünf anderen Ergebnisse, gewürfelt wird.
Weil die Ergebnisse eines Wahrscheinlichkeitsraumes in der Ergebnismenge festgelegt werden, muss bei der Frage, ob ein Laplace-Experiment vorliegt, auch immer die Ergebnismenge mit angegeben werden.
Laplace-Wahrscheinlichkeiten bestimmen
Aus der Bedingung, dass jedes Ergebnis gleich wahrscheinlich sein muss, folgt zusammen mit der allgemein geltenden Summenregel eine Regel, mit der sich Laplace-Wahrscheinlichkeiten oft leicht berechnen lassen.
Ist in einem Laplace-Experiment zum Beispiel Ω = {1; 2; 4; 6; 8} die Ergebnismenge, so muss jedes Ergebnis mit Wahrscheinlichkeit
15eintreten. Für die Wahrscheinlichkeit des Ereignisses E = {4; 6} folgt dann:
 P(E) = P({4}) + P({6}) =
15+
15=
25=
|E||Ω|
Um die Wahrscheinlichkeit eines Ereignisses zu berechnen, muss in Laplace-Experimenten lediglich das Verhältnis der Anzahl der enthaltenen Ergebnisse zur Anzahl aller möglichen Ergebnisse bestimmt werden.
P(E) = P({4}) + P({6}) =
15+
15=
25=
|E||Ω|
Um die Wahrscheinlichkeit eines Ereignisses zu berechnen, muss in Laplace-Experimenten lediglich das Verhältnis der Anzahl der enthaltenen Ergebnisse zur Anzahl aller möglichen Ergebnisse bestimmt werden.
 P(E) = P({4}) + P({6}) =
15+
15=
25=
|E||Ω|
Um die Wahrscheinlichkeit eines Ereignisses zu berechnen, muss in Laplace-Experimenten lediglich das Verhältnis der Anzahl der enthaltenen Ergebnisse zur Anzahl aller möglichen Ergebnisse bestimmt werden.
P(E) = P({4}) + P({6}) =
15+
15=
25=
|E||Ω|
Um die Wahrscheinlichkeit eines Ereignisses zu berechnen, muss in Laplace-Experimenten lediglich das Verhältnis der Anzahl der enthaltenen Ergebnisse zur Anzahl aller möglichen Ergebnisse bestimmt werden.
Formel:In einem Laplace-Experiment mit Ergebnismenge Ω gilt für die Wahrscheinlichkeit eines Ereignisses E:
P(E) =
Anzahl der für das Ereignis E günstigen ErgebnisseAnzahl der möglichen Ergebnisse=
|E||Ω|
Ein Ergebnis a ist genau dann günstig für ein Ereignis E, wenn es ein Element der Menge E ist: a ∈ E
Es bedeutet, dass das Ereignis beim entsprechenden Ergebnis eintreten würde.Für eine Menge E steht |E| übrigens für die Anzahl der enthaltenen Elemente.
Gib die Wahrscheinlichkeit für das Ereignis E = {rot; gelb} in einem Laplace-Experiment mit Ergebnismenge Ω = {grün; blau; rot; gelb; schwarz; weiß; rosa} an.
Laplace-Wahrscheinlichkeit
Du zählst die Elemente im Ereignis E (2) und in der Ergebnismenge Ω (7) und bildest den Quotienten.
P(E) =
27
Wenn du eine Wahrscheinlichkeit für ein Ereignis in einem Experiment bestimmen möchtest, das in einer Textaufgabe beschrieben wird, musst du zunächst feststellen was die Ergebnismenge ist oder wie du sie wählen kannst und ob damit ein Laplace-Experiment vorliegt oder nicht.
Beim Roulette wird eine Kugel in in ein Glücksrad mit von 0 bis 36 nummerierten und gleichmäßig verteilten Feldern gerollt. Wie groß ist die Wahrscheinlichkeit, mit der Kugel die 10, 20 oder 30 zu treffen?
Wähle zunächst aus, welche dieser Mengen du als Ergebnismenge Ω definieren kannst, um die gesuchte Wahrscheinlichkeit in einem Laplace-Experiment zu bestimmen.

Ergebnismenge bestimmen
Auf dem Rad sind alle Felder gleich groß und symmetrisch angeordnet. Also sind für Ω = {0; 1; 2; 3; …; 36} alle Ergebnisse gleich wahrscheinlich.
Insbesondere sind bei dieser Wahl von Ω auch die drei in der Aufgabe betrachteten Wurfergebnisse (10, 20 und 30) als Ergebnisse in der Menge enthalten, die gesuchte Wahrscheinlichkeit kann somit durch Abzählen bestimmt werden.
Bei Ω = {Vielfaches von 10; kein Vielfaches von 10} gäbe es lediglich 2 Ergebnisse, nämlich „10, 20 oder 30 treffen“ oder „weder 10 noch 20 noch 30 treffen“. Also könntest du dann lediglich unterscheiden, entweder eines von drei Feldern (10, 20 und 30) zu treffen oder eines der 34 anderen Felder. Dieses Experiment wäre kein Laplace-Experiment.
Gerade die Wahrscheinlichkeit des Ereignisses „10, 20 oder 30 treffen“ ist in dieser Aufgabe zu bestimmen, die Wahl von Ω = {Vielfaches von 10; kein Vielfaches von 10} eignet sich dafür aber nicht.

Antwort
Da hier ein Laplace-Experiment vorliegt, brauchst du lediglich das Verhältnis der Anzahl für das Ereignis günstiger Ergebnisse zur Anzahl aller möglichen Ergebnisse zu bestimmen.
Da es 37 verschiedene Möglichkeiten für das Ergebnis gibt und 3 davon günstig für das beschriebene Ereignis sind, ist die gesuchte Wahrscheinlichkeit P({10; 20; 30}) =
337.
Relative Häufigkeiten
Die relative Häufigkeit einer Eigenschaft bei Beobachtungen gibt das Verhältnis aus der Anzahl der Beobachtungen mit dieser Eigenschaft zur Gesamtanzahl aller Beobachtungen an.
Sie beschreibt also einen Anteil, der mindestens 0 und höchstens 1 beträgt.Als Anteil oder Verhältnis wird eine relative Häufigkeit als Dezimalzahl, oft aber auch in Prozent oder als Bruch dargestellt.
Relative Häufigkeit von A =
Anzahl der Beobachtungen mit der Eigenschaft AAnzahl aller Beobachtungen
Häufigkeiten bestimmen
Beim Fußballtraining hat Marc 18 von 25 Elfmetern verwandelt. Fabian hat 16 von 20 Elfmetern verwandelt.
Marc: - Anzahl aller Elfmeter: 25 - Absolute Häufigkeit der Treffer: 18 - Relative Häufigkeit der Treffer:
1825=
0.72= 72
%
Fabian: - Anzahl aller Elfmeter: 20 - Absolute Häufigkeit der Treffer: 16 - Relative Häufigkeit der Treffer:
1620=
0.8= 80
%
Obwohl Marc absolut mehr Elfmeter verwandelt hat, ist die relative Häufigkeit der Treffer bei Fabian größer.
Relative Häufigkeiten können also hilfreich beim Vergleich verschiedener Statistiken sein, wenn die Gesamtanzahl der Beobachtungen unterschiedlich ist.
In dieser Statistik sind 530 Mitglieder eines Vereins in drei Alterskategorien unterteilt:
- 104 Mitglieder sind 28 Jahre oder jünger. - 201 Mitglieder sind älter als 28 Jahre und höchstens 45 Jahre alt. - 225 Mitglieder sind über 45 Jahre alt.
Trage die relativen Häufigkeiten in diese Tabelle ein.


Relative Häufigkeiten bestimmen
Du bildest in den drei Spalten jeweils den Quotienten aus der absoluten Häufigkeit und der Gesamtanzahl der Mitglieder (530).Die Summe aller absoluten Häufigkeiten ergibt immer die Gesamtanzahl der betrachteten Elemente, hier also 530.Die Summe aller relativen Häufigkeiten ergibt immer 1, denn die Summe der Zähler ist gerade die Summe der absoluten Häufigkeiten:
104530+201530+225530=(104+201+225530)=530530=1


Absolute Häufigkeit schätzen
Du multiplizierst die berechnete relative Häufigkeit der Mitglieder über 45 mit der Gesamtanzahl der Mitglieder:
225530·636=(45106·636)=45·6=270
Achtung: Diese Art der Schätzung ist nur unter der erwähnten Voraussetzung an die Altersstruktur sinnvoll.
Von 106 weiteren Vereinsmitgliedern ist das Alter nicht bekannt.Gehe davon aus, dass die Altersstruktur aller 636 Mitglieder mit jener der 530 Mitglieder aus der Statistik übereinstimmt und schätze mit Hilfe der relativen Häufigkeiten, wie viele der insgesamt 636 Vereinsmitglieder über 45 Jahre alt sind.
Nach der berechneten relativen Häufigkeit sind 270 Vereinsmitglieder über 45 Jahre alt.
Wahrscheinlichkeiten schätzen
Kann für ein Ereignis eines Zufallsexperimentes keine genaue Wahrscheinlichkeit bestimmt werden, so kann man durch möglichst häufiges Durchführen dieses Experimentes eine Wahrscheinlichkeit schätzen. Dafür wird dann die beobachtete relative Häufigkeit benutzt:
Tritt ein Ereignis in beispielsweise 960 von 2000 identisch durchgeführten Versuchen ein, so geht man davon aus, dass dessen Wahrscheinlichkeit in diesem Experiment ungefähr
9602000= 48
%beträgt.
Umgekehrt wird angenommen, dass die relativen Häufigkeiten von Ereignissen mit steigender Anzahl der Versuche den tatsächlichen Wahrscheinlichkeiten immer häufiger beliebig nahe kommen.
Begründet werden diese Annahmen durch die Beobachtung, dass in sehr vielen Zufallsexperimenten die relativen Häufigkeiten bei steigender Anzahl der Versuche immer weniger schwanken.
Das nennt man auch das empirische Gesetz der großen Zahlen. Es kann nicht allgemein bewiesen werden und ist daher auch kein mathematischer Satz. Es ist eher eine Erfahrungstatsache und deutet überhaupt erst darauf hin, dass auch zufällige Erscheinungen gewissen Regelmäßigkeiten folgen.
Ein Autohersteller simuliert mit einem sogenannten Crashtest-Dummy als Fahrer des neuen Modells 2000-mal einen Auffahrunfall bei
30km/hund überprüft nach jedem Versuch, ob ein Mensch als Fahrer dabei verletzt worden wäre.
Dies sind die gezählten absoluten Häufigkeiten:
 Mit welcher Wahrscheinlichkeit wird nach dieser Statistik ein Fahrer dieses Autos bei einem vergleichbaren Unfall verletzt?
Mit welcher Wahrscheinlichkeit wird nach dieser Statistik ein Fahrer dieses Autos bei einem vergleichbaren Unfall verletzt?
Wahrscheinlichkeit schätzen
Für relative Häufigkeiten gelten übrigens dieselben Rechenregeln wie für Wahrscheinlichkeiten.
Da bei 684 von den 2000 Tests ein Fahrer verletzt worden wäre, ist die nach dieser Statistik zu schätzende WahrscheinlichkeitP(Verletzung) =
6842000= 34,2
%.
Sichere und unmögliche Ereignisse sowie Gegenereignisse
Zu jedem Ereignis E eines Zufallsexperimentes gibt es das sogenannte Gegenereignis
_E. Es besteht aus all denjenigen möglichen Ergebnissen des Zufallsexperimentes, die nicht zu E gehören.
Die Ergebnismenge Ω ist die Zusammenfassung aller möglichen Ergebnisse eines Zufallsexperimentes. Sie ist somit ebenfalls ein Ereignis. Da dieses Ereignis immer eintritt, nennt man dieses Ereignis auch sicheres Ereignis.
Das Gegenereignis zum sicheren Ereignis zeichnet sich durch die Abwesenheit möglicher Ergebnisse eines Zufallsexperimentes aus. Es ist also die leere Menge und wird mit ∅ bzw. { } bezeichnet. Man nennt ∅ bzw. { } das unmögliche Ereignis.
Ein Würfel mit den Augenzahlen 1, 2, 3, 4, 5 und 6 wird einmal geworfen. Weiterhin sei E das Ereignis „Eine Zahl größer oder gleich 3 wird gewürfelt“.
Das heißt, es ist E = {3; 4; 5; 6}.
Dann besteht das zu E gehörige Gegenereignis
_Eaus denjenigen Augenzahlen, die nicht zu E gehören. Somit gilt
_E= {1; 2}.
Ein Würfel mit den Augenzahlen 1, 2, 3, 4, 5 und 6 wird einmal geworfen. Bestimme das Gegenereignis
_Ezum gegebenen Ereignis E „Keine 4 wird gewürfelt“.








Gegenereignis bestimmen
Du wählst alle diejenigen Ergebnisse der Ergebnismenge aus, die nicht zu E gehören.Dies ist aber nur ein Ergebnis, und zwar das Ergebnis 4.

Ein Würfel mit den Augenzahlen 1, 2, 3, 4, 5 und 6 wird einmal geworfen. Weiterhin sei E das Ereignis „Eine positive Zahl wird gewürfelt ‟. Dann ist E das sichere Ereignis, denn jede würfelbare Augenzahl ist positiv.Das heißt, es ist E = {1; 2; 3; 4; 5; 6} = Ω.
 Es werden 2 Kugeln ohne Zurücklegen aus der abgebildeten Urne gezogen und E ist das Ereignis „Mindestens eine der Kugeln ist rot oder blau ‟.Entscheide, ob das beschriebene Ereignis E sicher, unmöglich oder zufällig ist.
Es werden 2 Kugeln ohne Zurücklegen aus der abgebildeten Urne gezogen und E ist das Ereignis „Mindestens eine der Kugeln ist rot oder blau ‟.Entscheide, ob das beschriebene Ereignis E sicher, unmöglich oder zufällig ist.
Ereignisart bestimmen
Das Ereignis ist sicher, da die gelbe Kugel nur einmal vorkommt und die gezogenen Kugeln nicht zurückgelegt werden.
Somit muss bei zwei gezogenen Kugeln immer eine dabei sein, die nicht gelb, also rot oder blau ist.

 Es werden 2 Kugeln ohne Zurücklegen aus der abgebildeten Urne gezogen und E ist das Ereignis „Beide Kugeln sind gelb ‟.Entscheide, ob das beschriebene Ereignis E sicher, unmöglich oder zufällig ist.
Es werden 2 Kugeln ohne Zurücklegen aus der abgebildeten Urne gezogen und E ist das Ereignis „Beide Kugeln sind gelb ‟.Entscheide, ob das beschriebene Ereignis E sicher, unmöglich oder zufällig ist.
Ereignisart bestimmen
Das Ereignis ist unmöglich, da die gelbe Kugel nur einmal vorkommt und die gezogenen Kugeln nicht zurückgelegt werden.


