Dreiecke, Vierecke und Kreise
Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13?
bettermarks bietet über 200.000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren. Ihre Schülerinnen und Schüler bekommen bei jedem Fehler eine personalisierte Rückmeldung und Sie erhalten Auswertungen zum Lernstand der Klasse.
Mehr erfahren- Flächeninhalt eines Rechtecks berechnen
- Flächeninhalt eines Quadrats berechnen
- Flächeninhalt einer rechtwinkligen Figur berechnen
- Umfang eines Rechtecks berechnen
- Flächeninhalt eines Dreiecks berechnen
- Allgemeines Dreieck und die Winkelsumme
- Haus der Vierecke
- Dreiecksarten und ihre Eigenschaften
- Flächeninhalt eines Kreises berechnen
- Kreisfläche in Sachzusammenhängen
- Umfang eines Kreises berechnen
- Kreisumfang in Sachzusammenhängen
Flächeninhalt eines Rechtecks berechnen
Um den
Flächeninhalt eines
Rechtecks zu bestimmen, kannst du es mit
Einheitsquadraten auslegen.
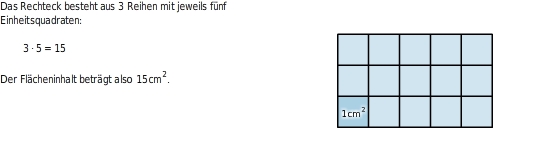
Allgemein erhältst du den Flächeninhalt (oder kurz die Fläche) A eines Rechtecks, wenn du die Länge a mit der Breite b multiplizierst:
A=a·b

Flächeninhalt eines Quadrats berechnen
Das
Quadrat ist ein besonderes
Rechteck.
Hier sind nicht nur die gegenüberliegenden Seiten gleich lang, sondern alle vier Seiten.
Für den Flächeninhalt A gilt dann:
A=a·a
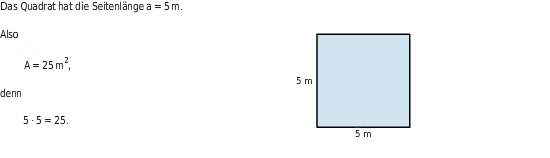
Flächeninhalt einer rechtwinkligen Figur berechnen
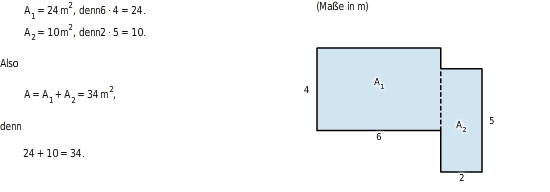
Im Alltag kommen häufig Flächen vor, die aus mehreren Rechtecken zusammengesetzt sind (zum Beispiel Wohnungsgrundrisse).
Auch für diese kannst du den Flächeninhalt berechnen.
Du überlegst zunächst, wie die Figur aus Rechtecken zusammengesetzt ist.
Dann berechnest du die Flächeninhalte dieser Rechtecke und addierst die Ergebnisse.
Umfang eines Rechtecks berechnen
Den
Umfang eines
Vielecks berechnest du, indem du alle Seitenlängen addierst.


Flächeninhalt eines Dreiecks berechnen
Den Flächeninhalt eines Dreiecks (A) berechnest du, indem du die Länge der Grundseite g mit der zugehörigen Höhe h multiplizierst und das Produkt durch 2 dividierst:
A=12g·h Da es drei verschiedene Grundseiten und die jeweiligen zugehörigen Höhen im Dreieck gibt, gibt es drei verschiedene Möglichkeiten den Flächeninhalt zu berechnen:Mit der Grundseite a:
A=12a·ha, wobei a die Länge der Seite a und
ha die zugehörige Höhe bezeichnet.Mit der Grundseite b:
A=12b·hb, wobei b die Länge der Seite b und
hb die zugehörige Höhe bezeichnet.Mit der Grundseite c:
A=12c·hc, wobei c die Länge der Seite c und
hc die zugehörige Höhe bezeichnet.
Den Flächeninhalt eines rechtwinkligen Dreiecks (A) berechnest du, indem du die Längen der Seiten, die den rechten Winkel einschließen, multiplizierst:
A=12a·b, wobei a und b die Längen der Seiten, die den rechten Winkel einschließen, bezeichnen.
Flächeninhalt eines Dreiecks:
A=12a·ha=12b·hb=12c·hc
Flächeninhalt eines rechtwinkligen Dreieck:
A=12a·b
Woher kommt die Formel zur Flächeninhaltsberechnung eines Dreiecks?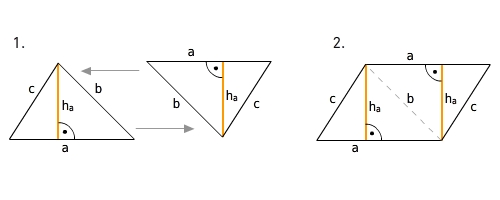

Wenn du zwei identische Dreiecke wie im Bild anlegst, erhältst du ein Parallelogramm. Daher ist der Flächeninhalt eines Dreiecks gleich der Hälfte des Flächeninhalts des erhaltenen Parallelogramms.
Woher kommt die Formel zur Flächeninhaltsberechnung eines rechtwinkligen Dreiecks?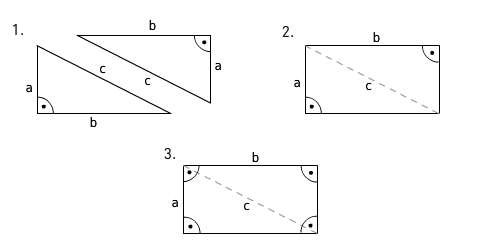

Wenn du zwei identische rechtwinklige Dreiecke wie im Bild anlegst, erhältst du ein Rechteck mit Länge a und Breite b. Daher ist der Flächeninhalt eines rechtwinkligen Dreiecks gleich der Hälfte des Flächeninhalts des Rechtecks.
Flächeninhalt eines Dreiecks
Berechne den Flächeninhalt des Dreiecks.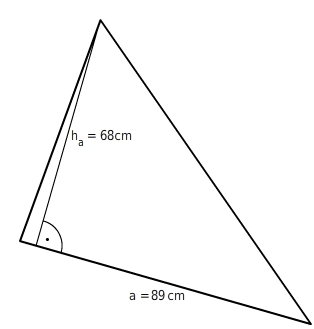

Flächeninhalt berechnen
Die Längen haben dieselbe Einheit. Du setzt die Werte in die Formel ein und erhältst so den Flächeninhalt des Dreiecks: 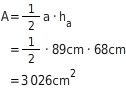

A=3026cm2
Flächeninhalt eines rechtwinkligen Dreiecks
Berechne den Flächeninhalt des Dreiecks.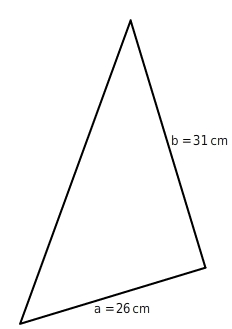

Flächeninhalt berechnen
Die Längen haben dieselbe Einheit. Du setzt die Werte in die Formel ein und erhältst so den Flächeninhalt des Dreiecks:  Der Flächeninhalt beträgt
403 cm2.
Der Flächeninhalt beträgt
403 cm2.
 Der Flächeninhalt beträgt
403 cm2.
Der Flächeninhalt beträgt
403 cm2.
A=403cm2
Allgemeines Dreieck und die Winkelsumme
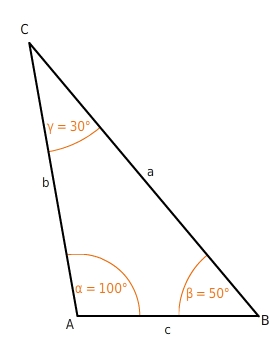
Ein Dreieck hat drei Eckpunkte, drei Seiten und drei Winkel.Für die Beschriftung der Eckpunkte eines Dreiecks verwendest du große Buchstaben in alphabetischer Reihenfolge (zum Beispiel A, B und C). Die Beschriftung erfolgt üblicherweise gegen den Uhrzeigersinn.
Die Seiten werden entsprechend mit kleinen Buchstaben (zum Beispiel a, b und c) beschriftet. Dabei liegt die Seite a dem Eckpunkt A gegenüber und verbindet die Punkte B und C.
Für Winkel werden kleine griechische Buchstaben verwendet (zum Beispiel α, β und γ). Dabei ist α der Winkel am Eckpunkt A, β liegt am Eckpunkt B und γ am Eckpunkt C. Die Summe der Innenwinkel eines Dreiecks beträgt
180°.

Winkelsumme: α + β + γ =
180°
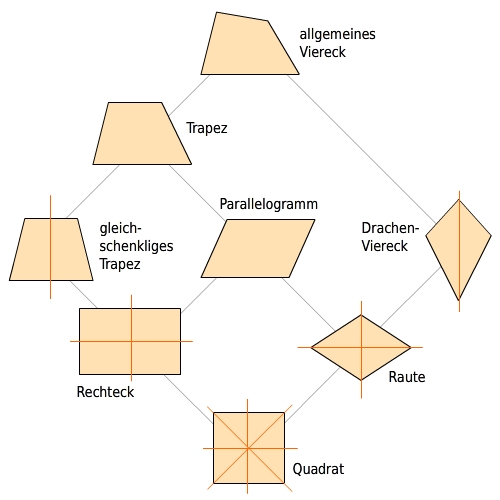
Haus der Vierecke
Das „Haus der Vierecke“ stellt die Beziehungen zwischen speziellen Vierecken dar.

Dreiecksarten und ihre Eigenschaften
Es gibt verschiedene Dreiecksarten. Du kannst diese nach der Größe ihrer Winkel und den Beziehungen ihrer Seitenlängen einteilen:
Winkelgröße:  Seitenlänge:
Seitenlänge:  Die Begriffe Winkelgröße und Seitenlänge lässt sich auch kombinieren (zum Beispiel „gleichschenklig-rechtwinkliges Dreieck“).
Die Begriffe Winkelgröße und Seitenlänge lässt sich auch kombinieren (zum Beispiel „gleichschenklig-rechtwinkliges Dreieck“).
 Seitenlänge:
Seitenlänge:
Spitzwinkliges Dreieck
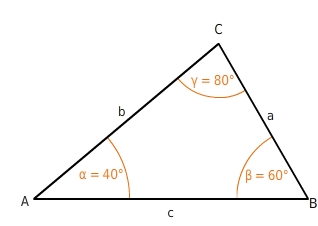

In einem spitzwinkligen Dreieck sind alle Winkel kleiner als
90°.
Rechtwinkliges Dreieck
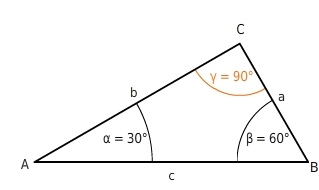

In einem rechtwinkligen Dreieck ist ein Winkel rechtwinklig, also genau
90° groß.
Rechte Winkel werden allgemein mit dem Symbol 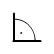 bezeichnet.
bezeichnet.
 bezeichnet.
bezeichnet.
Stumpfwinkliges Dreieck

In einem stumpfwinkligen Dreieck ist ein Winkel stumpf, also größer als
90°.
Gleichschenkliges Dreieck
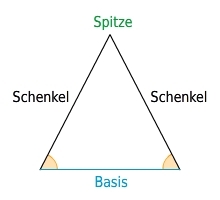

In einem gleichschenkligen Dreieck sind zwei Seiten (die beiden Schenkel) gleich lang. Der Schnittpunkt der beiden Schenkel heißt Spitze. Die dritte Seite wird Basis genannt und die beiden an der Basis anliegenden Winkel sind die Basiswinkel.
Spezielle gleichschenklige Dreiecke
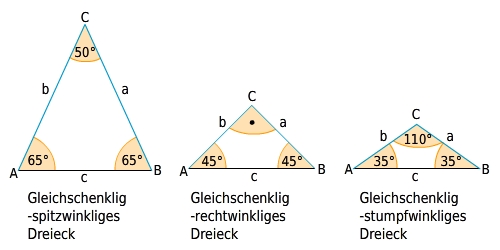

Gleichschenklig-spitzwinkliges Dreieck: zwei gleich lange Seiten und drei spitze Winkel (<
90°). Gleichschenklig-rechtwinkliges Dreieck: zwei gleich lange Seiten und ein rechter Winkel (
90°). Gleichschenklig-stumpfwinkliges Dreieck: zwei gleich lange Seiten und ein stumpfer Winkel (>
90°).
Gleichseitiges Dreieck


In einem gleichseitigen Dreieck sind alle Seiten gleich lang und alle Winkel gleichgroß (
60°).
Flächeninhalt eines Kreises berechnen
Die Formel für den Flächeninhalt eines Kreises kannst du unterschiedlich nutzen.
Wenn du zu gegebenem Radius
r den
FlächeninhaltAberechnen möchtest, setzt du den Wert für den Radius in die Formel ein und berechnest den Flächeninhalt.
Wenn du zu gegebenem Flächeninhalt
A den
Radiusrberechnen möchtest, stellst du die Formel nach
r um und setzt den Wert für
A in die umgestellte Formel ein:
A=pir2 r2=Api
r2=Api r=√Api
r=√Api
Berechne den Flächeninhalt des Kreises.
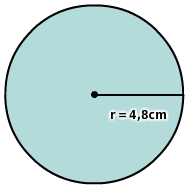 Gib das Ergebnis auf zwei Stellen nach dem Komma genau an.
Gib das Ergebnis auf zwei Stellen nach dem Komma genau an.
 Gib das Ergebnis auf zwei Stellen nach dem Komma genau an.
Gib das Ergebnis auf zwei Stellen nach dem Komma genau an.
Flächeninhalt berechnen
Du setzt den Radius
r=4.8cm in die Formel für die Kreisfläche ein:
 Das Endergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
A≈ 72,38
Achtung:In dieser Rechnung wurde für
pi der
pi-Wert des Taschenrechners genutzt. Rechnest du mit dem Näherungswert
3.14 für
pi, dann weicht dein Ergebnis etwas ab:
Das Endergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
A≈ 72,38
Achtung:In dieser Rechnung wurde für
pi der
pi-Wert des Taschenrechners genutzt. Rechnest du mit dem Näherungswert
3.14 für
pi, dann weicht dein Ergebnis etwas ab:

 Das Endergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
A≈ 72,38
Achtung:In dieser Rechnung wurde für
pi der
pi-Wert des Taschenrechners genutzt. Rechnest du mit dem Näherungswert
3.14 für
pi, dann weicht dein Ergebnis etwas ab:
Das Endergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
A≈ 72,38
Achtung:In dieser Rechnung wurde für
pi der
pi-Wert des Taschenrechners genutzt. Rechnest du mit dem Näherungswert
3.14 für
pi, dann weicht dein Ergebnis etwas ab:

Der Kreis hat einen Flächeninhalt von etwa
72.38cm2.
Berechne den Radius des Kreises. Der Kreis hat einen Flächeninhalt von
102m2.
Gib das Ergebnis auf zwei Stellen nach dem Komma genau an.
Radius berechnen
Du stellst die Formel für den Flächeninhalt nach r um:
A=pir2 r2=Api
r2=Api r=√Api
Dann setzt du 102 für
A in die umgestellte Formel ein:
r=√102pi
Führe die Division durch
pi und das Wurzelziehen durch, ohne zwischendurch zu runden:
r=5.6980...
Das Ergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
r≈
5.70
r=√Api
Dann setzt du 102 für
A in die umgestellte Formel ein:
r=√102pi
Führe die Division durch
pi und das Wurzelziehen durch, ohne zwischendurch zu runden:
r=5.6980...
Das Ergebnis rundest du auf die geforderte Anzahl an Stellen nach dem Komma:
r≈
5.70
Der Kreis hat einen Radius von etwa
5.70m.
Kreisfläche in Sachzusammenhängen
Eine kreisförmige Fläche entsteht oft durch ein rotierendes Objekt, zum Beispiel einen Wassersprenger. Hier ist es interessant zu wissen, wie groß die Fläche ist, die bewässert wird.
Um das Volumen bestimmter Körper (zum Beispiel Zylinder und Kegel) mit kreisförmiger Grundfläche berechnen zu können, benötigst du den Flächeninhalt dieser Grundfläche. Statt des Radius ist in diesen Fällen meist der Durchmesser gegeben, da sich dieser leichter messen lässt.

Der Meistergrill
5000 hat einen runden Grillrost mit einem Durchmesser von
60 cm. Ein Würstchen benötigt etwa
42 cm? Platz.
Wie viele Würstchen passen nebeneinander auf den Grillrost, wenn man die Fläche optimal ausnutzt?
Flächeninhalt des Grillrostes in cm" berechnen:
Der Radius (in cm) ist halb so groß wie der Durchmesser:
r=d2=602=30
Du setzt den Radius
r=
30cm in die Formel für den Flächeninhalt ein:
 Das Ergebnis rundest du auf ganze Quadratzentimeter:
A≈
2827
Anzahl der Würstchen berechnen:
Du dividierst den Flächeninhalt des Grillrosts
Das Ergebnis rundest du auf ganze Quadratzentimeter:
A≈
2827
Anzahl der Würstchen berechnen:
Du dividierst den Flächeninhalt des Grillrosts A = 2827 cm? durch den Platzbedarf pro Würstchen 42 cm? :
282742≈ 67,3
Auf den Grillrost passen bis zu 67 Würstchen.
 Das Ergebnis rundest du auf ganze Quadratzentimeter:
A≈
2827
Anzahl der Würstchen berechnen:
Du dividierst den Flächeninhalt des Grillrosts
Das Ergebnis rundest du auf ganze Quadratzentimeter:
A≈
2827
Anzahl der Würstchen berechnen:
Du dividierst den Flächeninhalt des Grillrosts Umfang eines Kreises berechnen
Aus dem Verhältnis des Kreisumfangs zum Kreisdurchmesser
Ud=π ergibt sich die Formel für die Berechnung des Umfangs eines Kreises bei gegebenem Durchmesser d:
U=πd
Hast du den Radius r des Kreises gegeben, verwendest du
U=π2r, denn
d=2r
Für den Umfang U eines Kreises mit dem Durchmesser d gilt:
U=πd
Für den Umfang U eines Kreises mit dem Radius r gilt:
U=2πr
Berechne den Umfang U des Kreises mit dem Radius r =
3.8cm. Runde das Ergebnis auf eine Stelle nach dem Komma.
Umfang berechnen
Den Umfang U berechnest du, indem du für den Radius in der Formel für den Kreisumfang den Wert 3,8 einsetzt:  Da du das Ergebnis auf eine Stelle nach dem Komma runden sollst, reicht es, vom genauen Ergebnis die ersten beiden Stellen nach dem Komma zu kennen. Oft reicht dafür schon der Näherungswert 3,14 für
π.
Da du das Ergebnis auf eine Stelle nach dem Komma runden sollst, reicht es, vom genauen Ergebnis die ersten beiden Stellen nach dem Komma zu kennen. Oft reicht dafür schon der Näherungswert 3,14 für
π.
 Da du das Ergebnis auf eine Stelle nach dem Komma runden sollst, reicht es, vom genauen Ergebnis die ersten beiden Stellen nach dem Komma zu kennen. Oft reicht dafür schon der Näherungswert 3,14 für
π.
Da du das Ergebnis auf eine Stelle nach dem Komma runden sollst, reicht es, vom genauen Ergebnis die ersten beiden Stellen nach dem Komma zu kennen. Oft reicht dafür schon der Näherungswert 3,14 für
π.
Der Kreis hat einen Umfang von etwa
23.9cm.
Berechne den Radius r eines Kreises mit dem Umfang
U=35.706m. Gib das Ergebnis auf Zentimeter genau an.
Radius berechnen
Du stellst die Formel für die Berechnung des Umfangs U nach r um und setzt 35,706 für U ein: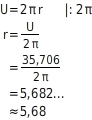 Für eine zentimetergenaue Angabe rundest du auf zwei Stellen nach dem Komma.Das sind
568 cm.
Für eine zentimetergenaue Angabe rundest du auf zwei Stellen nach dem Komma.Das sind
568 cm.
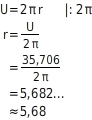 Für eine zentimetergenaue Angabe rundest du auf zwei Stellen nach dem Komma.Das sind
568 cm.
Für eine zentimetergenaue Angabe rundest du auf zwei Stellen nach dem Komma.Das sind
568 cm.
Der Kreis hat hat einen Radius von etwa
5.68m.
Kreisumfang in Sachzusammenhängen
Im Alltag hast du öfter mit kreisrunden Gegenständen zu tun, bei denen der Umfang von Interesse ist. Du kannst z.B. den Umfang eines Fahrradreifens berechnen und damit den zurückgelegten Weg bei einer bestimmten Anzahl von Radumdrehungen und daraus die Geschwindigkeit ermitteln.
Beim Longieren benutzt Emma eine Longierleine, die
8m lang ist. Welche Strecke hat das Pferd nach 25 Runden zurückgelegt" Gib das Ergebnis auf ganze Meter gerundet an.


Umfang berechnen
Zunächst berechnest du die Länge der Laufbahn, also den Umfang U des Longierkreises.Du setzt den Wert 8 für r in die Umfangsformel ein: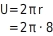 Das Pferd läuft 25 Runden:
Das Pferd läuft 25 Runden: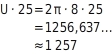 Das sind
1.257km.
Das sind
1.257km.
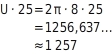 Das sind
1.257km.
Das sind
1.257km.
Die Laufstrecke des Pferdes beträgt etwa
1257m.
Philipp besitzt ein 24-Zoll-Fahrrad. Wenn Philipp damit fährt, dreht sich der Reifen durchschnittlich 105 Mal pro Minute. Mit welcher Geschwindigkeit ist Philipp unterwegs?Gib das Ergebnis auf Kilometer pro Stunde gerundet an.
Geschwindigkeit berechnen
Um die Geschwindigkeit v bestimmen zu können, benötigst du die Strecke s, die Philipp in t Minuten zurücklegt, denn
v=st. Die in einer Minute (
t=1) zurückgelegte Strecke s ist das 105-fache des Reifenumfanges U, den du mit der Umfangsformel berechnen kannst.Die Angabe „24 Zoll“ ist das Maß für den Durchmesser des Reifens (1 Zoll =
2.54cm).
Durchmesser des Reifens (in cm):  Umfang des Reifens (in cm):
Umfang des Reifens (in cm): Da sich der Reifen pro Minute 105 Mal dreht, legt Philipp in einer Minute eine Strecke (in cm) zurück, die dem 105-fachen des Umfangs entspricht:
105·191.51=20108.55
Eine Stunde hat 60 Minuten, also schafft es Philipp in einer Stunde 60-mal so weit:
20108.55·60=1206,513
Du gibst das Ergebnis mit der geforderten Genauigkeit in km an:
Da sich der Reifen pro Minute 105 Mal dreht, legt Philipp in einer Minute eine Strecke (in cm) zurück, die dem 105-fachen des Umfangs entspricht:
105·191.51=20108.55
Eine Stunde hat 60 Minuten, also schafft es Philipp in einer Stunde 60-mal so weit:
20108.55·60=1206,513
Du gibst das Ergebnis mit der geforderten Genauigkeit in km an: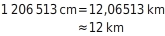
 Da sich der Reifen pro Minute 105 Mal dreht, legt Philipp in einer Minute eine Strecke (in cm) zurück, die dem 105-fachen des Umfangs entspricht:
105·191.51=20108.55
Eine Stunde hat 60 Minuten, also schafft es Philipp in einer Stunde 60-mal so weit:
20108.55·60=1206,513
Du gibst das Ergebnis mit der geforderten Genauigkeit in km an:
Da sich der Reifen pro Minute 105 Mal dreht, legt Philipp in einer Minute eine Strecke (in cm) zurück, die dem 105-fachen des Umfangs entspricht:
105·191.51=20108.55
Eine Stunde hat 60 Minuten, also schafft es Philipp in einer Stunde 60-mal so weit:
20108.55·60=1206,513
Du gibst das Ergebnis mit der geforderten Genauigkeit in km an:
Philipp erreicht eine Geschwindigkeit von etwa
12km/h.

