Karten, Maßstab und Symmetrie
Lerninhalte
- Planquadrate als Orientierungshilfe nutzen
- Maßstäbliches Vergrößern und Verkleinern
- Kennenlernen der Begriffe Parallel, Senkrecht, Lotrecht und Waagerecht
- Aufgaben zur Achsen- und Drehsymmetrie, sowie zur Verschiebung
Orientieren mit Planquadraten
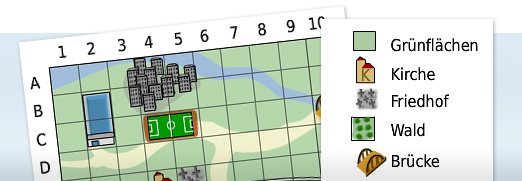In den unterschiedlichsten Aufgaben müssen Objekte auf Planquadraten ihrer exakten Position zugeordnet werden.
Mit Maßstäben rechnen
Mit Abbildungen und Maßstabsangaben werden reale Längen berechnet.
Die Grundbegriffe der Geometrie
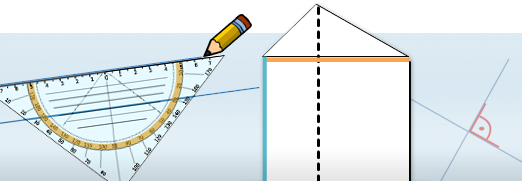Begriffe wie Parallel, Senkrecht, Lotrecht und Waagerecht treten in verschiedensten Zusammenhängen auf.